Предмет: Геометрия,
автор: sadwriter
СРОЧНО ПОМОГИТЕ
Пусть радиусы двух окружностей равны 1 и 2, а расстояние между их центрами равно 10. Чему равно расстояние от центра меньшей окружности до точки пересечения радикальной оси и линии центров?
задача из сириуса
Ответы
Автор ответа:
7
Ответ:
4,85 ед.
Объяснение:
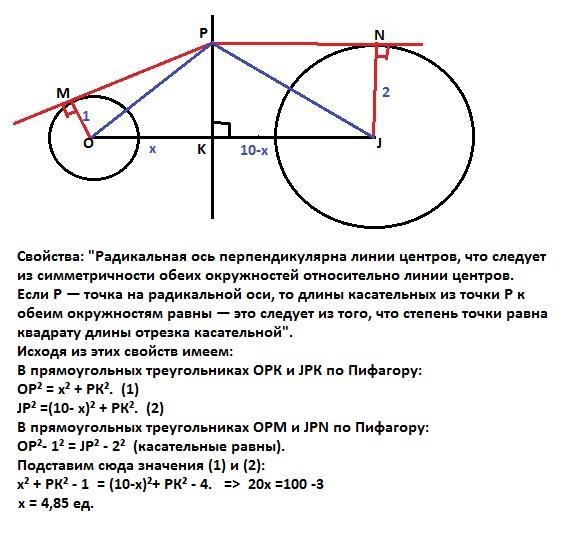
Свойства: "Радикальная ось перпендикулярна линии центров, что следует из симметричности обеих окружностей относительно линии центров.
Если P — точка на радикальной оси, то длины касательных из точки P к обеим окружностям равны — это следует из того, что степень точки равна квадрату длины отрезка касательной".
Исходя из этих свойств имеем:
В прямоугольных треугольниках ОРК и JРК по Пифагору:
ОР² = х² + РК². (1)
JР² =(10- х)² + РК². (2)
В прямоугольных треугольниках ОРМ и JPN по Пифагору:
ОР²- 1² = JP² - 2² (касательные равны).
Подставим сюда значения (1) и (2):
х² + РК² - 1 = (10-х)²+ РК² - 4. => 20x =100-3.
х = 4,85 ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: irakar25
Предмет: Русский язык,
автор: natka061007
Предмет: Русский язык,
автор: Lenal1003
Предмет: Математика,
автор: 1YuriKOkay1
Предмет: Математика,
автор: кошка384