Предмет: Алгебра,
автор: yyyyiiii
Даю 35 баллов помогите решить пример
Приложения:
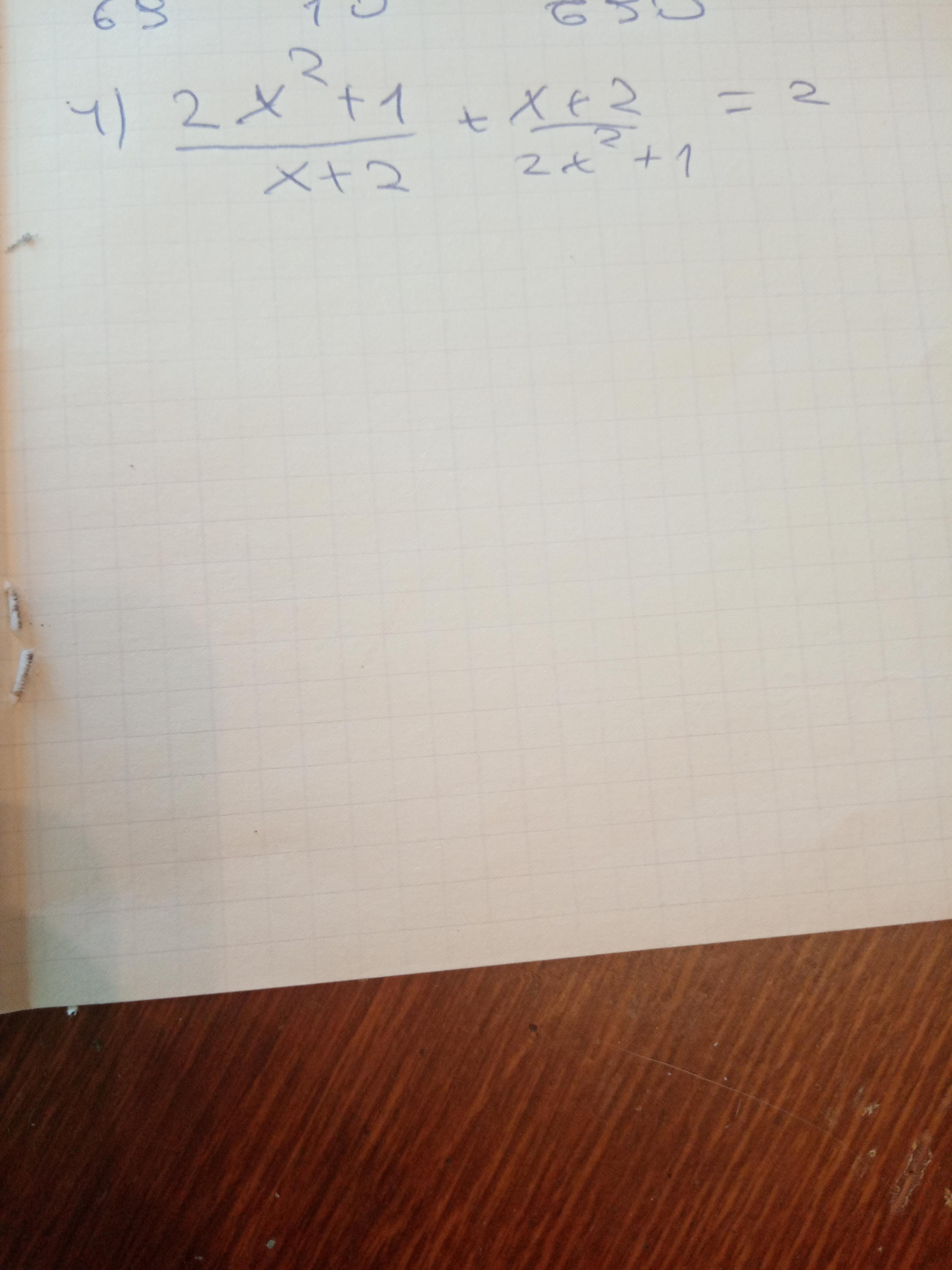
Ответы
Автор ответа:
0
Ответ:
(2x^2+1)/(x+2)+(x+2)/(2x^2+1) = (общий множитель) (2x^2+1)*(2x^2+1)/(x+2)*(2x^2+1)+(x+2)*(x+2)/(2x^2+1)*(x+2) = (4x^4+2x^2+2x^2+1)/(2x^3+x+4x^2+2)+(x^2+2x+2x+4)/(2x^3+x+4x^2+2) = (4x^4+4x^2+1)/(2x^3+x+4x^2+2)+(x^2+4x+4)/(2x^3+x+4x^2+2) = (единая дробная черта) (4x^4+4x^2+1)+(x^2+4x^2+4)/(2x^3+x+4x+2)+(2x^3+x+4x+2) = (4x^4+4x^2+1+x^2+4x^2+4)/(2x^3+x+4x^2+2+2x^3+x+4x+2) = (4x^4+9x^2+5)/(4x^3+6x+4x^2+4)
Похожие вопросы
Предмет: Русский язык,
автор: saidadadulaeva
Предмет: Английский язык,
автор: tanya220278
Предмет: Русский язык,
автор: 12082006
Предмет: Химия,
автор: dashcotowa2017
Предмет: Математика,
автор: mihail301