Question

Даны плоскость α и не пересекающий данную плоскость отрезок AB. На этом отрезке взята точка C так, что AC : CB = 3 : 2. Найдите расстояние (cm) от точки C до плоскости α, если расстояния из концов отрезка AB до плоскости равны AA1=18 cm и BB1=13 cm.

Answer 1

Даны плоскость α и не пересекающий данную плоскость отрезок AB. На этом отрезке взята точка C так, что AC : CB = 3 : 2. Найдите расстояние (cm) от точки C до плоскости α, если расстояния из концов отрезка AB до плоскости равны AA1=18 cm и BB1=13 cm.

Пошаговое объяснение:

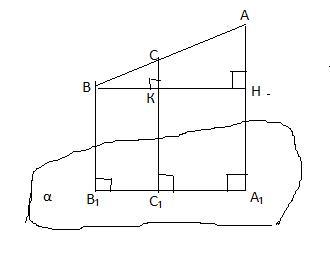
Т.к.  AC : CB = 3 : 2 ,то  АВ составляет 5 частей, ВС-две части отрезка АВ.

Т.к. в задаче идет речь о расстояниях , то АА₁⊥α,  СС₁⊥α , ВВ₁⊥α ⇒ АА₁║СС₁║ВВ₁.

Пусть ВН⊥АА₁  ⇒АН=18-13=5 (см)  . Отрезок СС₁=СК+КС₁  .

ΔАВН подобен ΔСВК по 2 углам :∠В -общий,∠ВКС=∠ВНА=90° ⇒ сходственные стороны пропорциональны :

$\frac{5}{CK} =\frac{5}{2} ,$  СК=2 см.

СС₁=2+13=15 (см)