Question

найти наименьший период функции y(x)=sin(cosx)

Answer 1

Фуркция y=f(x)  называется периодической, если

существует Т > 0  такое, что f(x+T)=f(x) для любого х ∈D(f)

Данная функция является композицией двух функций:

y=sin(cos(x))

Функция  t=cosx -  периодическая с периодом Т =2π,

т.е верно равенство:  

cos(x+2π)=cosx

для любого х ∈(-∞;+∞)

Проверим выполнимость равенства

sin(cos(x+T))=sin(cosx)  для T=2π

sin(cos(x+2π))=sin(cosx)  - верно.

О т в е т. Т=2π

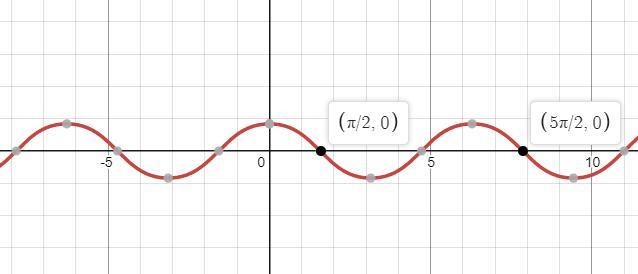
cм рис  график y=sin(cosx):