Предмет: Математика,
автор: bokarevstefan475
Нужно подробное решение данного неравенства. Срочно!
Приложения:
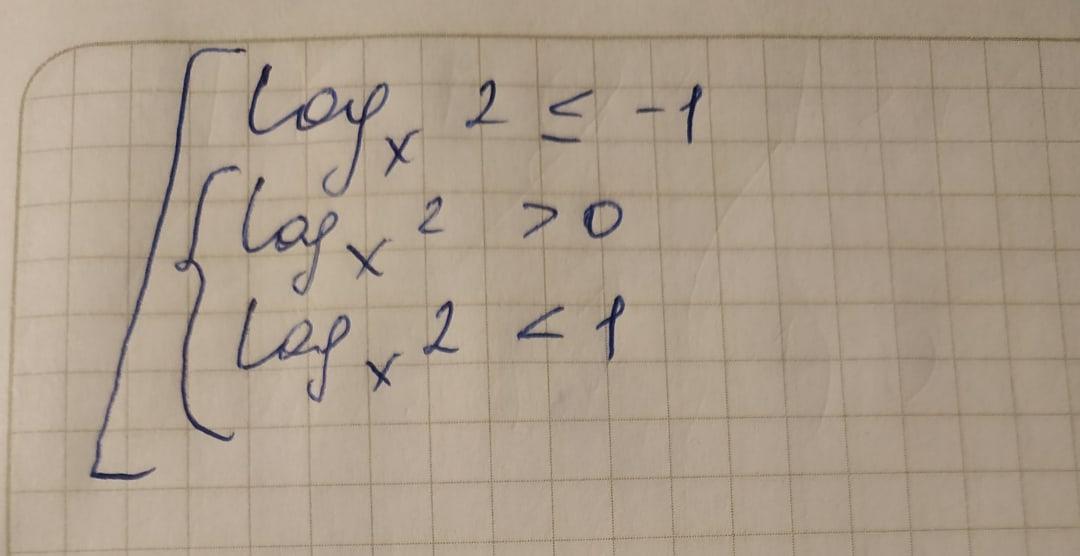
нукасин:
они не противоречат, квадратная скобка = или
Ответы
Автор ответа:
0
Запишем одз: так как 2>0 то достаточно чтобы x≠1 и х>0
Так же logx(2)=1/log2(x)
Перепишем так систему (фигурная скобка):01, после возведения 2 в эту степень выйдет х>2(знаки сохраняются потому что 2^x больше если больше степень (если число между 0 и 1 то знаки пришлось бы менять но мы возводим 2 в степень))
Logx(2)<=-1 перепишем так -1<=log2(x)<0(если число меньше минус 1 то обратное между -1 и 0 а если число -1 то обратное -1) возводим 2 в эту степень 2^-1<=х<2^0(знаки сохраняются об этом уже говорилось) тогда 1/2<=х<1
Выходит объединение [1/2;1) и (2;+бесконечность)
Ответ объединение [1/2;1) и (2;+бесконечность)
Так же logx(2)=1/log2(x)
Перепишем так систему (фигурная скобка):01, после возведения 2 в эту степень выйдет х>2(знаки сохраняются потому что 2^x больше если больше степень (если число между 0 и 1 то знаки пришлось бы менять но мы возводим 2 в степень))
Logx(2)<=-1 перепишем так -1<=log2(x)<0(если число меньше минус 1 то обратное между -1 и 0 а если число -1 то обратное -1) возводим 2 в эту степень 2^-1<=х<2^0(знаки сохраняются об этом уже говорилось) тогда 1/2<=х<1
Выходит объединение [1/2;1) и (2;+бесконечность)
Ответ объединение [1/2;1) и (2;+бесконечность)
Так почему до 1 не включительно?
В самом начале по одз х≠1
Единица откуда получается? Из log x 2 < 0?
Область допустимых значений(доз) для логарифма loga(b):a>0 b>0 a≠1
a и b больше 0 и а не равняется 1
Хорошо, тогда почему у нас x не может быть, скажем, 1.5?
Если x=1,5 то logx(2) больше 1
Справедливо
Автор ответа:
0
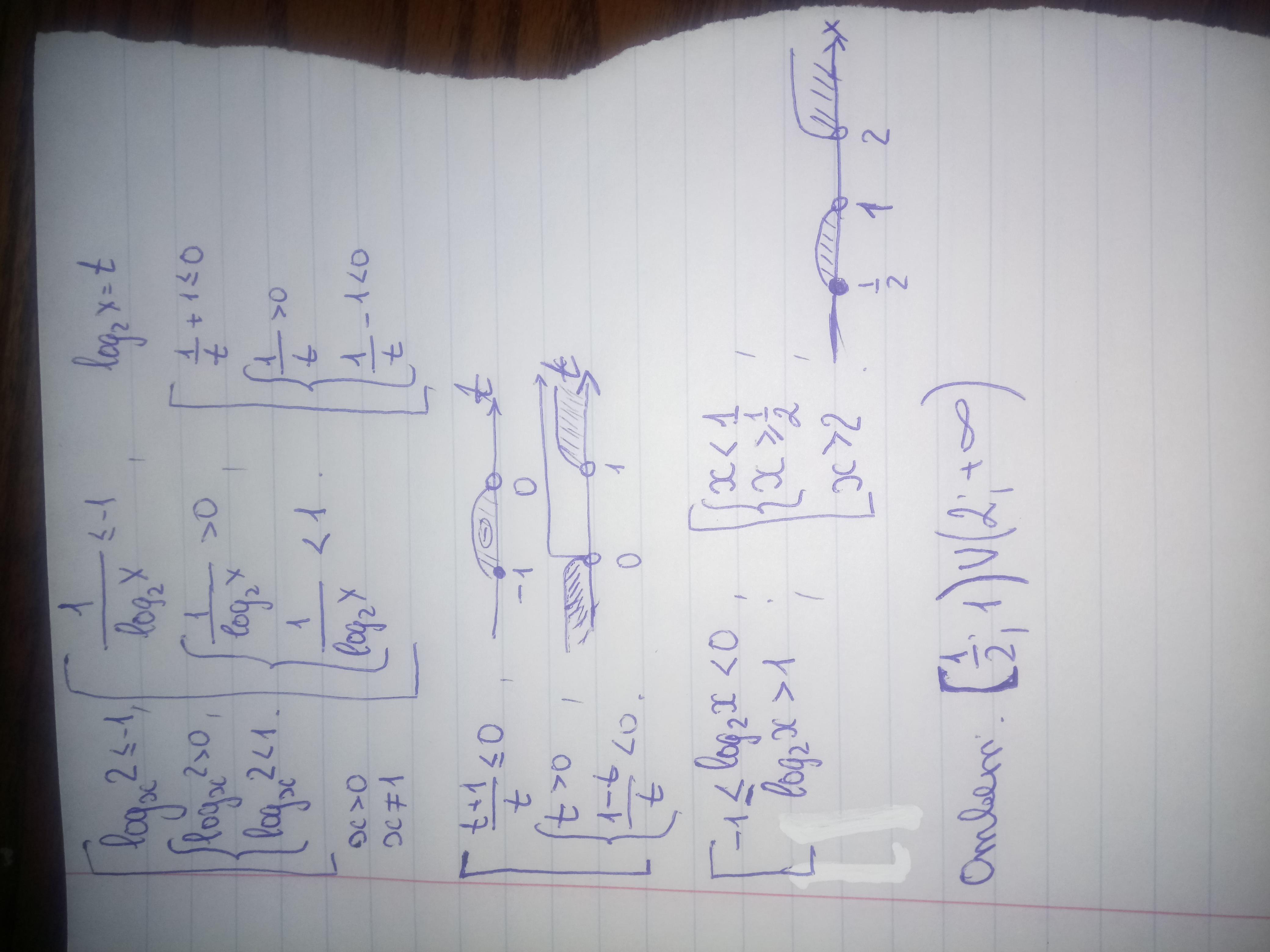
Решение объединения неравенства и системы прилагаю.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 3655678
Предмет: Русский язык,
автор: МашаПляшем
Предмет: Русский язык,
автор: albiertgalimov
Предмет: Алгебра,
автор: Странник1111
Предмет: Литература,
автор: kola41