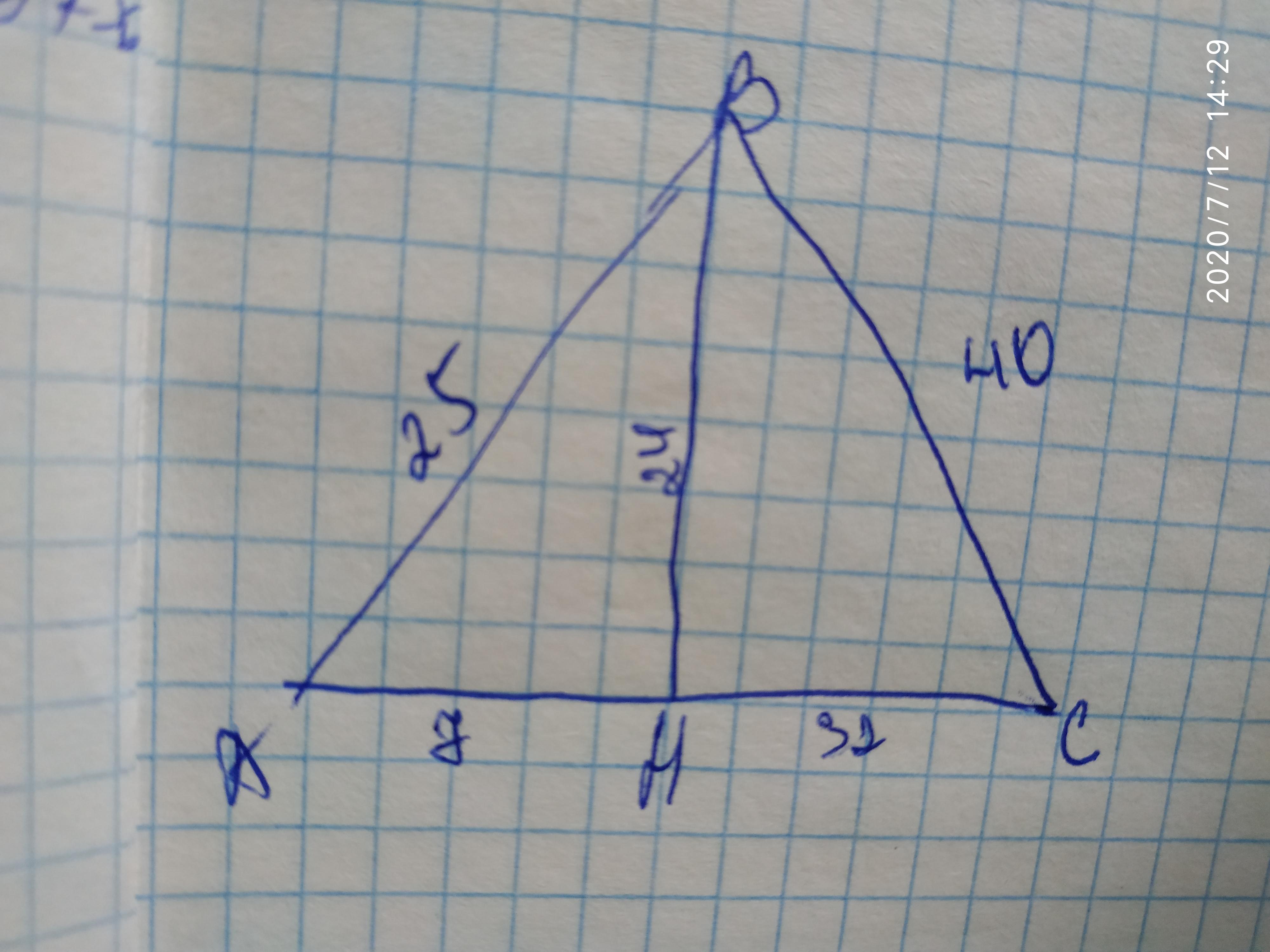
У трикутнику із сторонами 25 і 40 см з вершини кута між ними проведено висоту, яка ділить третю його сторону на відрізки, менший з яких дорівнює 7 см. Обчисліть периметр трикутника.
Ответы
Ответ:104 см
Объяснение:
Пусть треугольник АВС. АВ=25 см , ВС=40 см, ВН (высота)=?,
АН=7см
Из треугольника АВН по т Пифагора найдем ВН.
ВН= sqrt (AB^2- AH^2)=sqrt(625-49)=24 см
Тогда из треугольника ВНС по т Пифагора находим НС=sqrt(BC^2-BH^2)
HC=sqrt(1600-576)=sqrt(1024)=32
AC=HC+AH=7+32=39 см
P=25+40+39=104 см
Ответ:
104 см
Объяснение:
Дано
Трикутник ∆АВС
АВ=25 см
ВС=40 см
АН=7
ВН=? висота
АС=? сторона трикутника
Р∆АВС=? периметр трикутника
Рішення.
∆АВН прямокутний, ВН і АН - катети.
АВ- гіпотенуза.
За теоремою Піфагора знайдемо ВН
ВН²=АВ²-АН²=25²-7²=625-49=576 см
ВН=√576=24 см.
∆ВНС- прямокутний, ВН і НС - катети, ВС- гіпотенуза.
За теоремою Піфагора знайдемо НС
НС²=ВС²-ВН²=40²-24²=1600-576=1024 см
НС=√1024=32 см
АС=АН+НС=7+32=39 см
Р∆АВС=АВ+ВС+АС=25+40+39=104 см периметр трикутника.
Відповідь: периметр трикутника дорівнює 104 см