Question

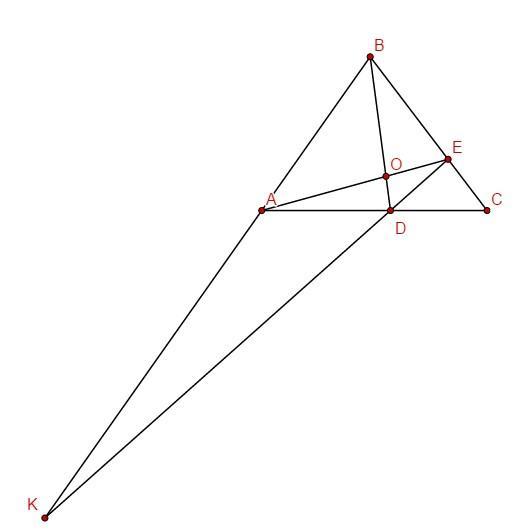
Точка D лежит на стороне AC треугольника ABC, точка E на стороне BC. Известно: AD:DC = 4:3, BE:EC = 2:1. а) Отрезки AE и BD пересекаются в точке О. Найдите отношения AO:OE и BO:OD б) Прямая DE пересекает прямую AB в точке К. Найдите отношение AK:AB

Answer 1

По теореме Менелая для треугольника $AEC$ :

$\dfrac{CD}{AD}\cdot \dfrac{AO}{OE}\cdot \dfrac{BE}{BC}=1~\Leftrightarrow~ \dfrac{3x}{4x}\cdot \dfrac{AO}{OE}\cdot \dfrac{2y}{3y}=1~\Rightarrow~ \boxed{ \dfrac{AO}{OE}=2}$

По теореме Менелая для треугольника $BDC:$

$\dfrac{CE}{BE}\cdot \dfrac{BO}{OD}\cdot \dfrac{DA}{AC}=1~\Leftrightarrow~ \dfrac{y}{2y}\cdot \dfrac{BO}{OD}\cdot \dfrac{4}{7}=1~\Rightarrow~ \boxed{\dfrac{BO}{OD}=\dfrac{7}{2}}$

По теореме Менелая для треугольника $ABC$ :

$\dfrac{BE}{EC}\cdot \dfrac{CD}{DA}\cdot \dfrac{AK}{KB}=1~\Leftrightarrow~ \dfrac{2y}{y}\cdot \dfrac{3x}{4x}\cdot \dfrac{AK}{AK+AB}=1~\Rightarrow~ \boxed{\dfrac{AK}{AB}=2}$