Предмет: Алгебра,
автор: runcupa21
Найдите наибольшее целое значение параметра а, при котором уравнение имеет единственное решение.
х3 + ах2 + (a + 3) х = 0
Ответы
Автор ответа:
0
Выразим а через х:
Строим графики
и y =a
y=a - прямая, параллельная оси Ох
Область определения: x²+x≠0 ⇒ x(x+1)≠0 ⇒ x≠0; x≠-1
Строим график функции с выколотой точкой с абсциссой 0 ( см. обл опр.)
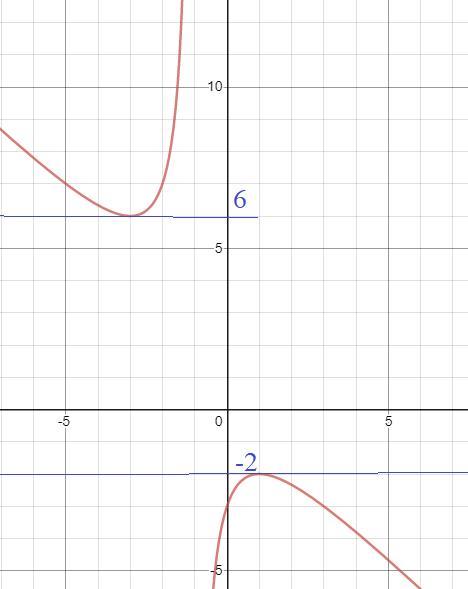
По графику прямая y=a пересекается с графиком в одной точке
при a=6 или a=-2
Наибольшее a=6
О т в е т. a=6
Приложения:
nafanya2014:
точка (0;-3) должна быть выколотой
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: aizhanaset
Предмет: Русский язык,
автор: juliabar82
Предмет: Математика,
автор: princessamimimii
Предмет: География,
автор: русалочка01рая