Предмет: Алгебра,
автор: delfamasterua2k18
сроооооочоно 9 завдання
Приложения:
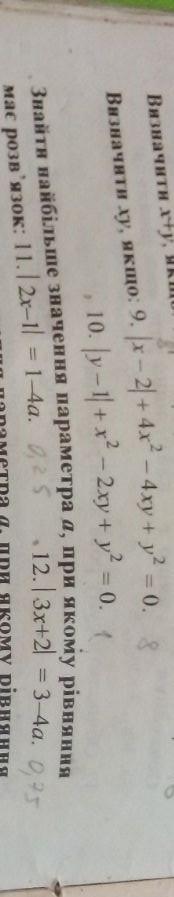
Ответы
Автор ответа:
2
Задание 9.
Заметим, что три последних слагаемых образуют квадрат разности (формула ):
Первое слагаемое неотрицательно (из-за модуля), второе - тоже неотрицательно (из-за квадрата). ⇒ Их сумма тоже неотрицательна.
Но по условию, она равна . Значит, каждое слагаемое равно
.
Получаем:
Отсюда . Задача решена!
Ответ: 8.
Похожие вопросы
Предмет: Русский язык,
автор: mishasorokin0
Предмет: Русский язык,
автор: verabessonova2
Предмет: Русский язык,
автор: drhous
Предмет: Литература,
автор: Irinunicorn15
Предмет: Алгебра,
автор: KarinaMS