Предмет: Математика,
автор: anonim6918
Помогите пожалуйста
Приложения:
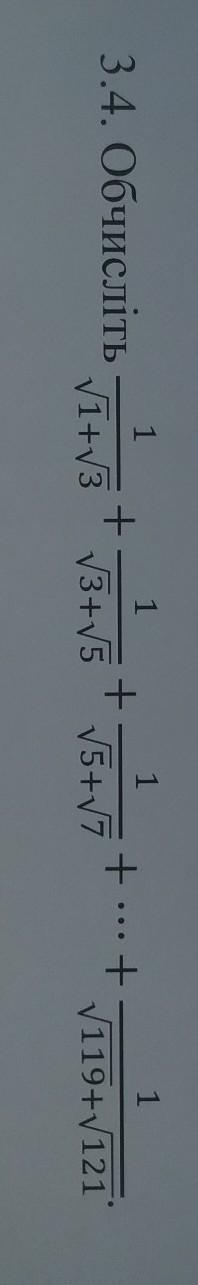
Ответы
Автор ответа:
1
Избавление от иррациональности в знаменателе:k/(sqrt(a)+ sqrt(b)=k*(sqrt(a)-sqrt(b))/((sqrt(a)+ sqrt(b))(sqrt(a)-sqrt(b)))= k*(sqrt(a)-sqrt(b))/(a-b)
Избавимся от иррациональности в знаменателе с помощью формулы разности квадратов:1/(sqrt(k)+sqrt(k+2))=(sqrt(k+2)-sqrt(k))/(k+2-k)=(sqrt(k+2)-sqrt(k))/2теперь у всех этих дробей знаменатель=2 тогда сумма будет из-за того что числители теперь суммировать такой:(sqrt(3)-sqrt(1)+ sqrt(5)-sqrt(3)+....+sqrt(119)-sqrt(117)+ sqrt(121)-sqrt(119))/2 можно заметить что в числителе всё сократиться кроме sqrt(121) и sqrt(1) выходит изначальная сумма будет иметь вид (sqrt(121)-sqrt(1))/2=(11-1)/2=10/2=5
Ответ:5
Избавимся от иррациональности в знаменателе с помощью формулы разности квадратов:1/(sqrt(k)+sqrt(k+2))=(sqrt(k+2)-sqrt(k))/(k+2-k)=(sqrt(k+2)-sqrt(k))/2теперь у всех этих дробей знаменатель=2 тогда сумма будет из-за того что числители теперь суммировать такой:(sqrt(3)-sqrt(1)+ sqrt(5)-sqrt(3)+....+sqrt(119)-sqrt(117)+ sqrt(121)-sqrt(119))/2 можно заметить что в числителе всё сократиться кроме sqrt(121) и sqrt(1) выходит изначальная сумма будет иметь вид (sqrt(121)-sqrt(1))/2=(11-1)/2=10/2=5
Ответ:5
Похожие вопросы
Предмет: Русский язык,
автор: EVDOWENKO2014
Предмет: Русский язык,
автор: Dragunov2222
Предмет: Английский язык,
автор: Ilhama
Предмет: Математика,
автор: GAzOnOKosilKa
Предмет: Математика,
автор: ane4kakolesova