Предмет: Алгебра,
автор: Vladocik2017
ПОМОГИТЕ РЕШИТЬ ЭТО УРАВНЕНИЕ,ПОЖАЛУЙСТА!
Приложения:
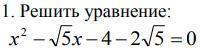
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
Значит:
или
откуда получаем два корня:
и
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: dkfjhg
Предмет: Қазақ тiлi,
автор: ritta4444
Предмет: История,
автор: chmilyulya
Предмет: Химия,
автор: engkalinino