Предмет: Алгебра,
автор: wiwejep842
Решите уравнение 35 баллов
Приложения:
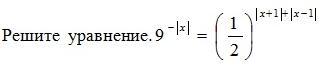
mozgmira62:
напишите текстом,пожалуйста,фото не открывается
извени это нериальео
тем более для 4 класса
Ответы
Автор ответа:
0
Ответ:
x1 = -log_9 (4); x2 = log_9 (4)
Объяснение:
1) Для x < -1 будет: -|x| = x; |x+1| = -x-1; |x-1| = 1-x
Это уравнение имеет один корень x = 0, но он > -1 и не подходит.
Поэтому при x < -1 решений нет.
2) Для x ∈ [-1; 0) будет: -|x| = x; |x+1| = x+1; |x-1| = 1-x
∈ [-1; 0) - ЭТО РЕШЕНИЕ.
3) Для x ∈ [0; 1) будет -|x| = -x; |x+1| = x+1; |x-1| = 1-x
∈ [0; 1) - ЭТО РЕШЕНИЕ.
4) Для x >= 1 будет -|x| = -x; |x+1| = x+1; |x-1| = x-1
Это уравнение имеет один корень x = 0, но он < 1 и не подходит.
Похожие вопросы
Предмет: Английский язык,
автор: санёк2004
Предмет: Русский язык,
автор: polina210205
Предмет: Английский язык,
автор: a3520243
Предмет: Алгебра,
автор: noora25
Предмет: Литература,
автор: 1ЛілЯ111