Предмет: Математика,
автор: albina1795
Доказать, что для всех натуральных n верно неравенство:
Приложения:
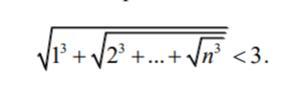
Ответы
Автор ответа:
3
Пусть последовательность такова, что для всех
выполнено неравенство
. Тогда верно неравенство
. Это легко видеть, заменяя члены с использованием неравенства.
В нашем случае , неравенство
верно для всех натуральных
. Значит, искомая сумма не превосходит
. Для
очевидно.
polka125:
В первом неравенстве n и m в каких отношениях находятся?
так, я начинаю что-то понимать
а, нет, показалось
а, всё, всё понял, великолепное решение, побольше бы таких
При доказательстве использовалось неравенство: корень (2(к+1)^3)<=k^3. Как то доказать? Вынесла вопрос отдельной задачей.
Похожие вопросы
Предмет: Русский язык,
автор: mavlonov00
Предмет: Русский язык,
автор: sumiy
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: 28965