Предмет: Алгебра,
автор: kriv4a
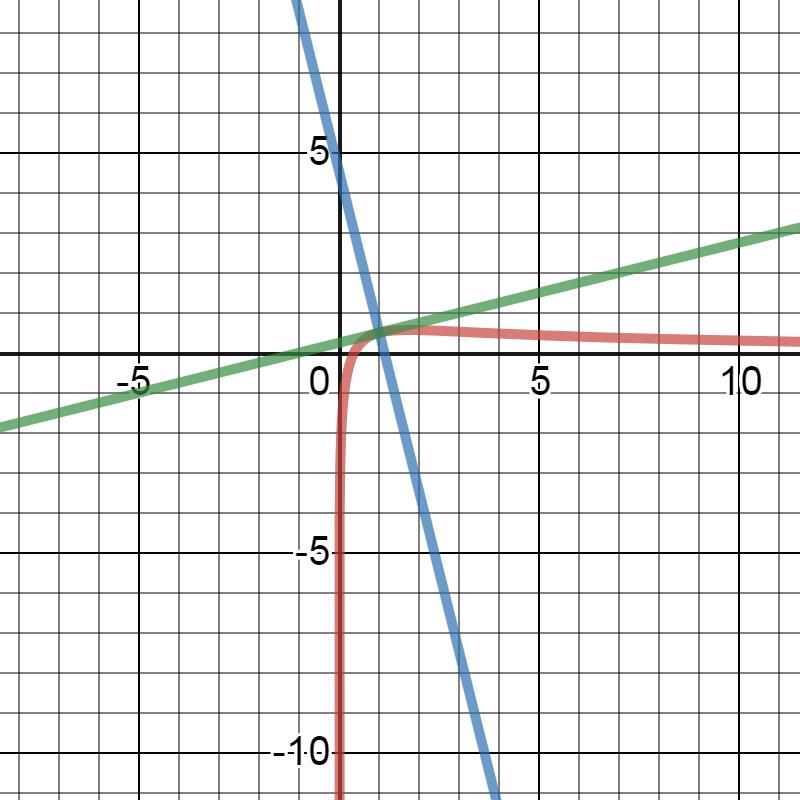
Дана функция y=(㏑x+1)/(x+1) и значение x0=1 Найти уравнения касательной и нормали к графику функции y=f(x) в точке с абсциссой х0. Построить графики функции, касательной и нормали в окрестности точки (х0, f(х0)).
Ответы
Автор ответа:
1
Ответ:
Объяснение:
yk - зелёный, yn - синий, y - красный.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: fotik73
Предмет: Русский язык,
автор: v727nn
Предмет: Українська мова,
автор: 6tyu
Предмет: Химия,
автор: мамкаааа