Предмет: Геометрия,
автор: skuzevanov89
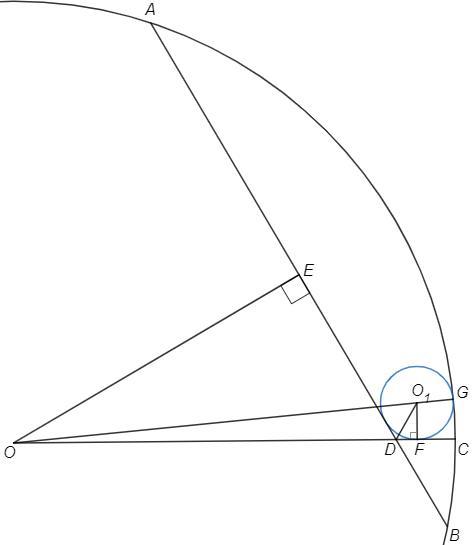
Дана окружность радиуса 2√3 с центром в точке О. Хорда АВ пересекает радиус ОС в точке D, причём угол CDA=120 градусов. Известно, что OD=3. а) Докажите, что расстояние от точки О до хорды АВ равно 3√3/2. б) Найдите радиус окружности, вписанной в угол ADC и касающейся дуги АС.
Ответы
Автор ответа:
5
a) Расстояние измеряется длиной перпендикуляра.
ODA =180-ADC =60
OE =OD*sin(ODA) =3√3/2
б) F, G - точки касания.
Центр O1 искомой окружности лежит на биссектрисе угла ADC.
O1DC =ADC/2 =60
DF =O1F/tg(O1DC) =r/√3
OF =OD+DF =3 +r/√3
Точка касания G лежит на линии центров.
OO1 =OG-O1G =2√3 -r
Теорема Пифагора, △OO1F
OO1^2 =O1F^2 +OF^2
(2√3 -r)^2 =r^2 +(3 +r/√3)^2
r^2 +18√3*r -9 =0
r =6√7 -9√3
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Kate1vk
Предмет: Другие предметы,
автор: kzrctq
Предмет: Русский язык,
автор: emiliyalevchen
Предмет: Алгебра,
автор: mronichan