Question

СРОЧНО!ПОМОГИТЕ РЕШИТЬ ЗАДАНИЕ 9!!!!!

Answer 1

Наибольшее значение функция примет тогда, когда знаменатель будет минимальным.

Рассмотрим сумму $|x-2|+|x+2|$, чтобы узнать, при каких $x$ она примет наименьшее значение. Разобьём её на 3 интервала:

Первый

$x \geq 2\\x-2+x+2=2x$

Второй

$-2 \leq x \leq 2\\2-x+x+2=4$

Третий

$x \le -2\\2-x-x-2=-2x$

В первом и во втором случае сумма может принимать сколь угодно большое значение. Поэтому нам подходит второй интервал. Подставим значение икса в нашу формулу - подходит любое значение из интервала $-2 \leq x \leq 2$. Допустим, ноль:

$y=\dfrac{5}{|0-2|+|0+2|+1}=\dfrac{5}{2+2+1}=1$

Ответ: 1 (при $-2 \leq x \leq 2$)

Answer 2

Ответ: 1

Объяснение:

y= 5/( |x-2| +|x+2| +1)

|x-2| +|x+2| >0 ,таким образом,  функция принимает наибольшее значение, когда знаменатель  минимален.

То  есть :  |x-2| +|x+2|  должно быть минимальным.

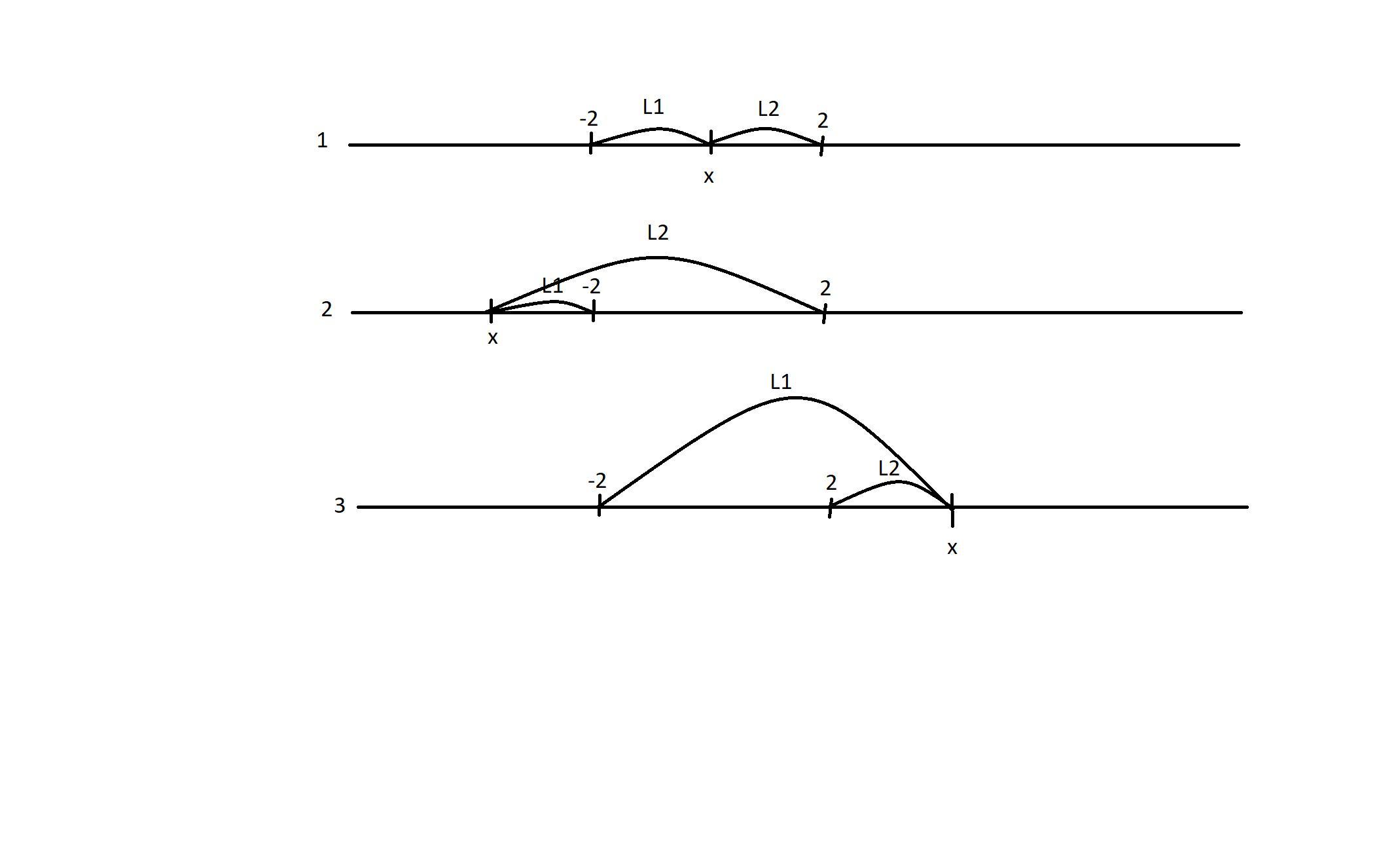
Выражения  |x-2| и |x+2| представляют расстояния от точки x до точек 2 и -2.

|x+2| = L1 ;  |x-2| =L2;

На рисунке показаны все случаи расположения x.

Во втором и третьем случае , очевидно, что : L1+L2 = 2*L1 +4>=4  ( во втором случае)  и L1+L2= 2*L2+ 4>=4  (в третьем случае).   При этом расстояния L1 и L2 неограниченны во втором и третьем случае.

Таким образом  значение L1+L2 в первом и третьем случае неограниченно растет.

В первом  случае :  L1+L2 = 4

Таким образом :

min(|x-2| и |x+2|) = 4

Тогда :

max(5/( |x-2| +|x+2| +1) ) = 5/5 = 1