Предмет: Алгебра,
автор: sashasluzhaev2001
Найти точки перегиба графика функции y=e^(1/x)
Ответы
Автор ответа:
0
Найдем вторую производную функции:
Вторая производная обращается в ноль при
Вторая производная не существует при
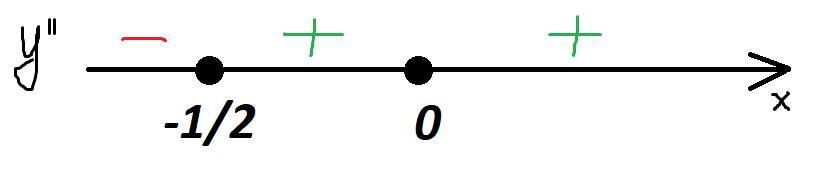
Рассмотрим знаки второй производной (картинка).
Как видно, при переходе через точку вторая производная меняет знак. Значит, это и есть точка перегиба.
Ответ: -1/2
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: olgamihaylova
Предмет: Русский язык,
автор: Аноним
Предмет: Українська література,
автор: manamana180
Предмет: Геометрия,
автор: Jek15