Предмет: Математика,
автор: наташка2016
Решить с 1 по 6. Легкие баллы
Приложения:

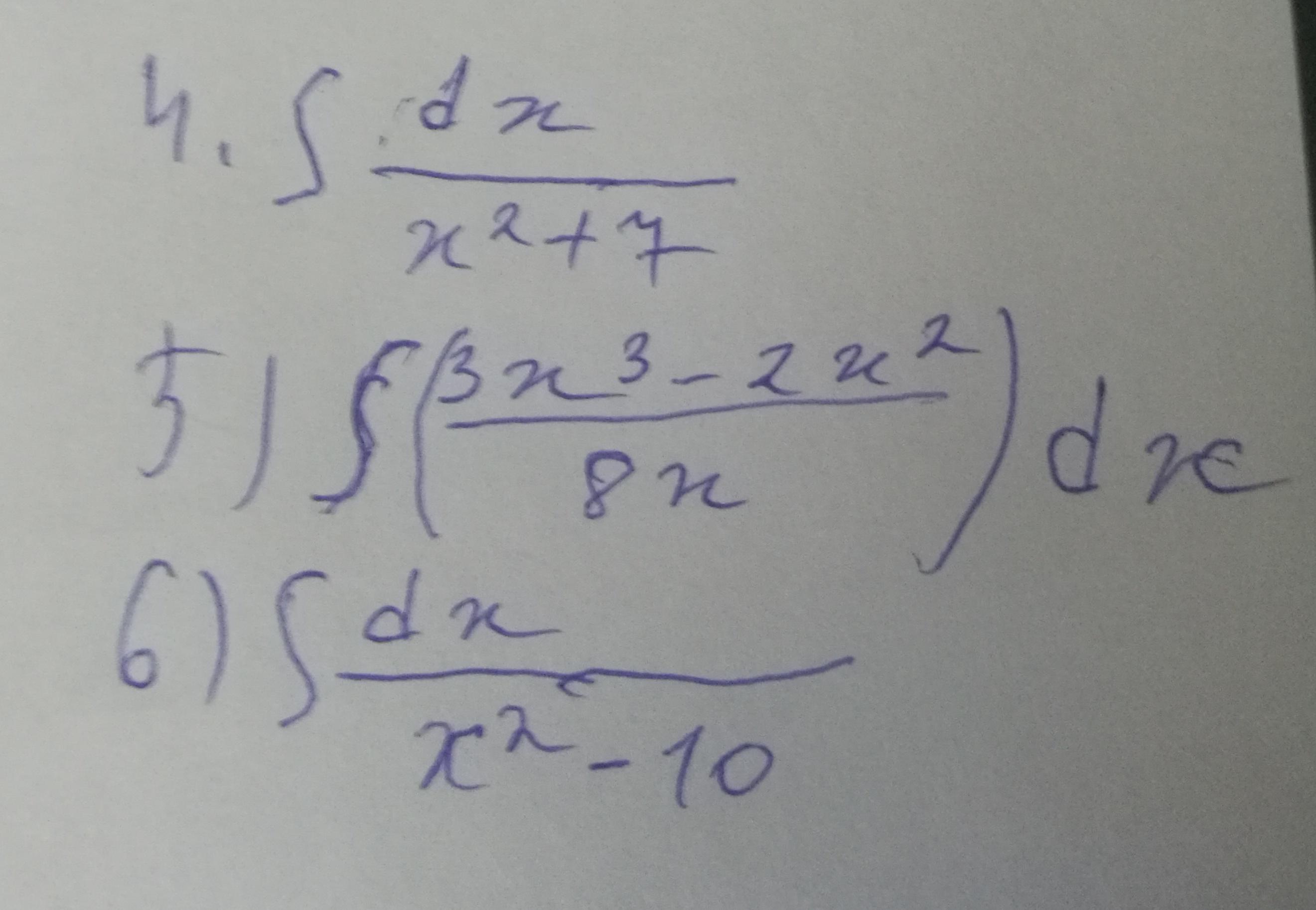
наташка2016:
найти интегралы, используя таблицу и основные свойства
Ответы
Автор ответа:
0
Ответ:
NNNLLL54, распиши подробнее
Похожие вопросы
Предмет: Русский язык,
автор: suzi355
Предмет: Українська мова,
автор: lenasavinova8
Предмет: Английский язык,
автор: MTiffani
Предмет: История,
автор: kuznetsovserge
Предмет: Алгебра,
автор: rgrgg