Предмет: Алгебра,
автор: Jackoe89
Вычислить данный предел
Приложения:
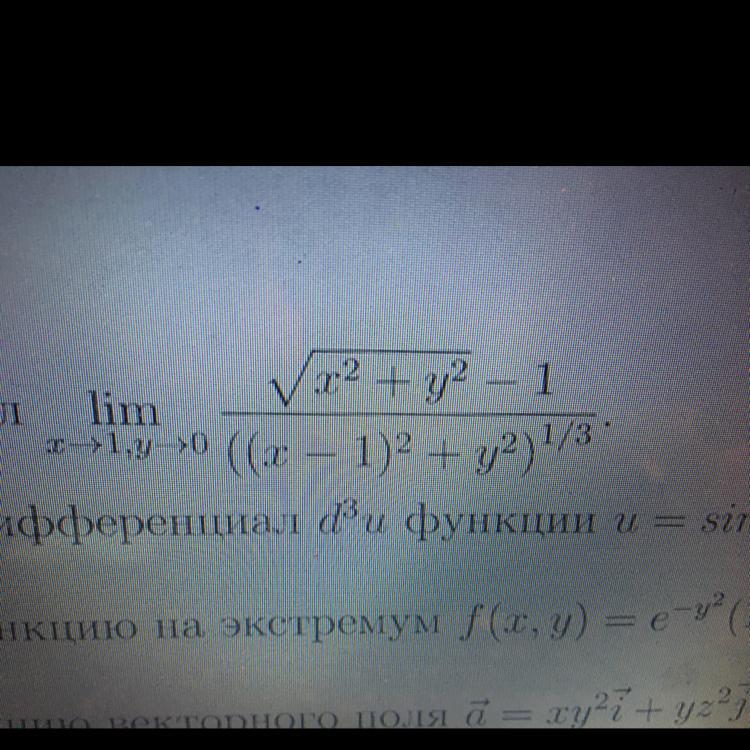
Ответы
Автор ответа:
1
Сделаем замену: . Получим:
. Теперь можно сделать другую замену:
,
. После преобразований выйдет:
. Теперь зажмем функцию под пределом между
и
. Взяв предел от этих частей, получим, что искомый предел равен 0.
Похожие вопросы
Предмет: Русский язык,
автор: динис11
Предмет: Русский язык,
автор: skif2690
Предмет: Русский язык,
автор: лвтлвытгтвгыо
Предмет: Биология,
автор: Dencccccc
Предмет: Математика,
автор: anuta3030