Предмет: Математика,
автор: voronin188
Помогите решить, пожалуйста
Приложения:
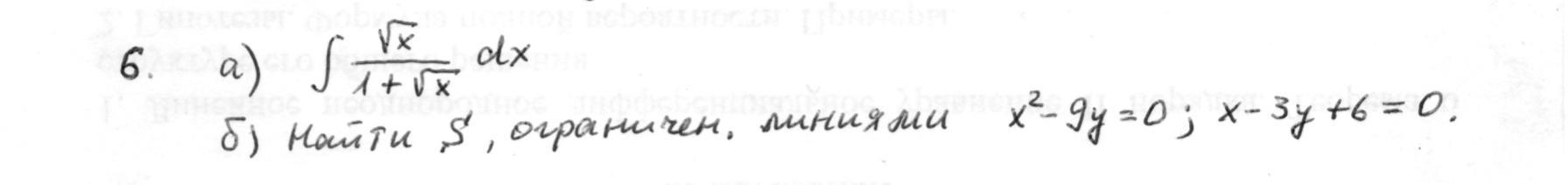
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
a)
=u² - 2u + 2 ln(u+1) +C = [обратная замена} = x - 2√x + 2ln (1+√x) +C
б)
x²-9y=0; x-3y +6=0;
y₂ = x²/9; y₁ = (x+6)/3
найдем точки пересечения
x²/9 = (x+6)/3 ⇒ x²-3x-18=0 ⇒x₁ = -3; x₂ = 6
теперь площадь
Похожие вопросы
Предмет: Қазақ тiлi,
автор: anetaa
Предмет: Русский язык,
автор: daska114
Предмет: Русский язык,
автор: дринара1222
Предмет: Математика,
автор: lagytina24