Предмет: Математика,
автор: vodneva1803
Помогите решить, пожалуйста
Приложения:

Ответы
Автор ответа:
0
Пошаговое объяснение:
7.
8.
Пусть cosx=t ⇒ |t|≤1
Ответ: x=π+2πn, n∈Z.
9.
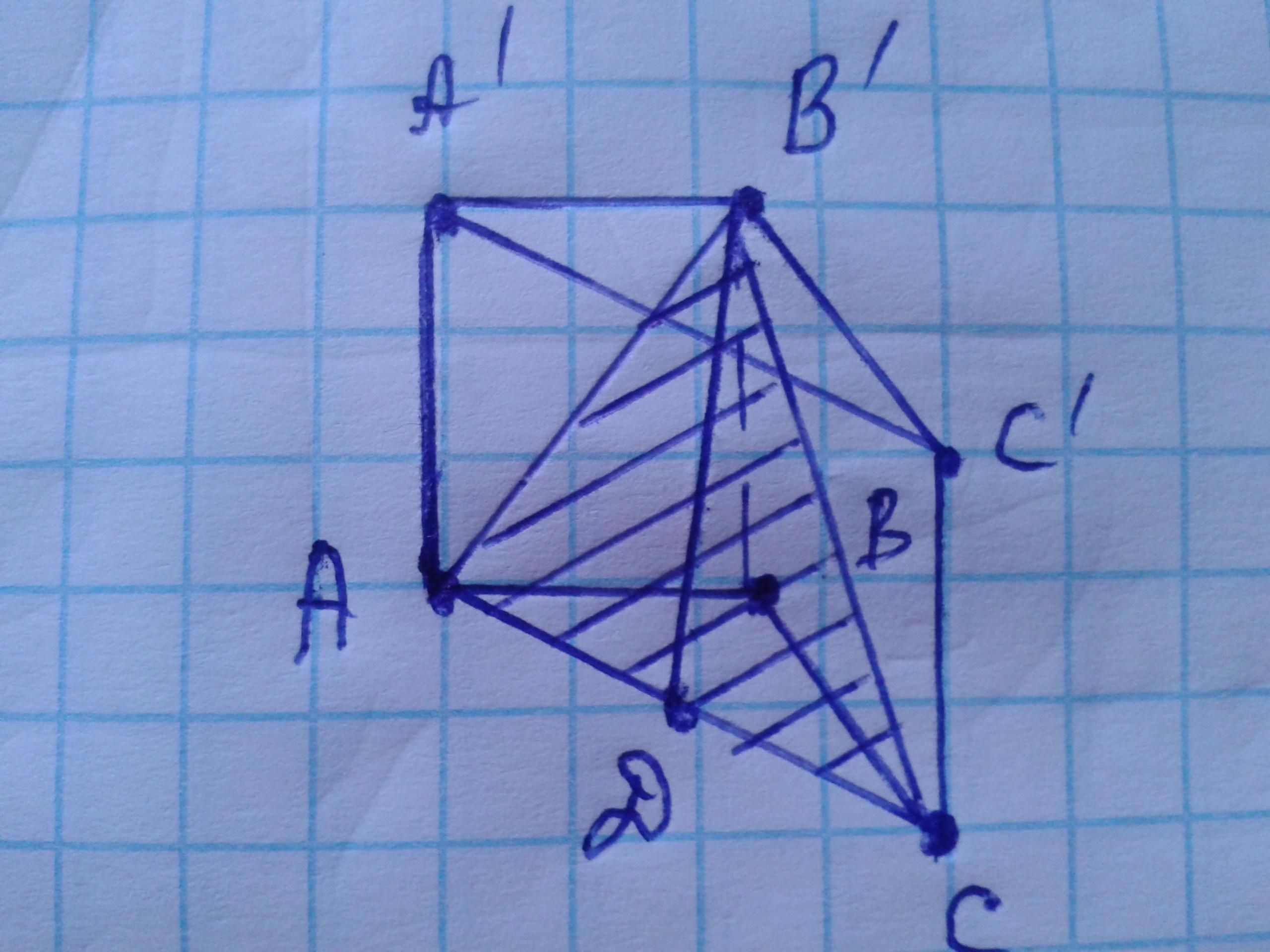
AC=12 см AA'=6 см Sab'c=?
Диагональ грани АВ'²=AB²+AA'²=12²+6²=144+36=180.
Высота B'D=√(AB'²-(AC/2)²)=√(180-(12/2)²)=√(180+6²)=
=√(180-36)=√144=12 (cм). ⇒
Sab'c=12*12/2=12*6=72 (см²).
Ответ: площадь сечения Sab'c=72 cм².
10.
ОДЗ: x^2-3x≠0 x*(x-3)≠0 x≠0 x≠3.
Пусть x²-3x=t ⇒
Ответ: x₁=-1 x₂=4 x₃=1 x₄=2.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: valef2012
Предмет: Английский язык,
автор: danylka
Предмет: Английский язык,
автор: Настюша055
Предмет: Химия,
автор: dianabxj