Помогите решить , пожалуйста(неравенства)
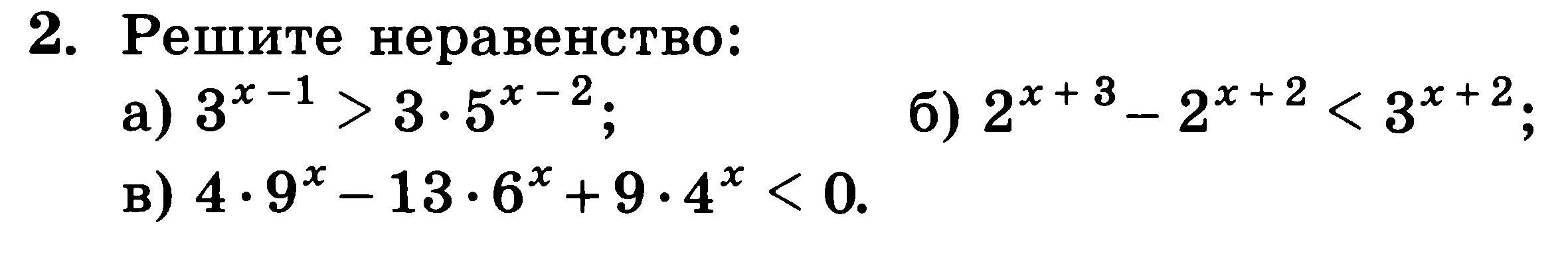
Ответы
Ответ:
Пошаговое объяснение:
а) 3ˣ⁻¹>3·5ˣ⁻²
Допустим:
3ˣ⁻¹=3·5ˣ⁻²
3ˣ⁻¹/3=5ˣ⁻²
3ˣ⁻¹⁻¹=5ˣ⁻²
3ˣ⁻²=5ˣ⁻²
3ˣ⁻²=5ˣ⁻²
x-2=0
x=2
При x>2: 3³⁻¹>3·5³⁻²; 3²>3·5; 9<15 - неравенство не выполняется.
При x<2: 3¹⁻¹>3·5¹⁻²; 1>3/5; 1>0,6 - неравенство выполняется.
Следовательно, x∈(-∞; 2).
б) 2ˣ⁺³-2ˣ⁺²<3ˣ⁺²
Допустим:
2ˣ⁺³-2ˣ⁺²=3ˣ⁺²
2ˣ(2³-2²)=3ˣ⁺²
2ˣ·4=3ˣ⁺²
2ˣ⁺²=3ˣ⁺²
x+2=0; x=-2
При x>-2: 2⁻¹⁺³-2⁻¹⁺²<3⁻¹⁺²; 4-2<3; 2<3 - неравенство выполняется.
При x<-2: 2⁻³⁺³-2⁻³⁺²<3⁻³⁺²; 1 -1/2<1/3; 3/6>2/6 (3>2) - неравенство не выполняется.
Следовательно, x∈(-2; +∞).
в) 4·9ˣ-13·6ˣ+9·4ˣ<0
Допустим:
4·9ˣ-13·6ˣ+9·4ˣ=0 |4ˣ
4·(9/4)ˣ-13·(6/4)ˣ+9·(4/4)ˣ=0
4·(9/4)ˣ-13·(3/2)ˣ+9=0; (3/2)ˣ=t
4t²-13t+9=0; D=169-144=25
t₁=(13-5)/8=8/8=1; (3/2)ˣ=1; (3/2)ˣ=(3/2)⁰; x₁=0
t₂=(13+5)/8=18/8=9/4=(3/2)²; (3/2)ˣ=(3/2)²; x₂=2
При x>0: 4·9¹-13·6¹+9·4¹<0; 36-78+36<0; 72-78<0; -6<0 - неравенство выполняется.
4·9³-13·6³+9·4³<0 |4
729-13·54+9·16<0; 729-702+144<0; 171>0 - неравенство не выполняется.
При x<2: 4·9¹-13·6¹+9·4¹<0; -6<0 - неравенство выполняется.
Следовательно, 0<x<2⇒x∈(0; 2).
Ответ: