Предмет: Алгебра,
автор: Jackoe89
Найти обратную матрицу
Приложения:

Ответы
Автор ответа:
0
Решение на прикреплённом изображении.
Приложения:
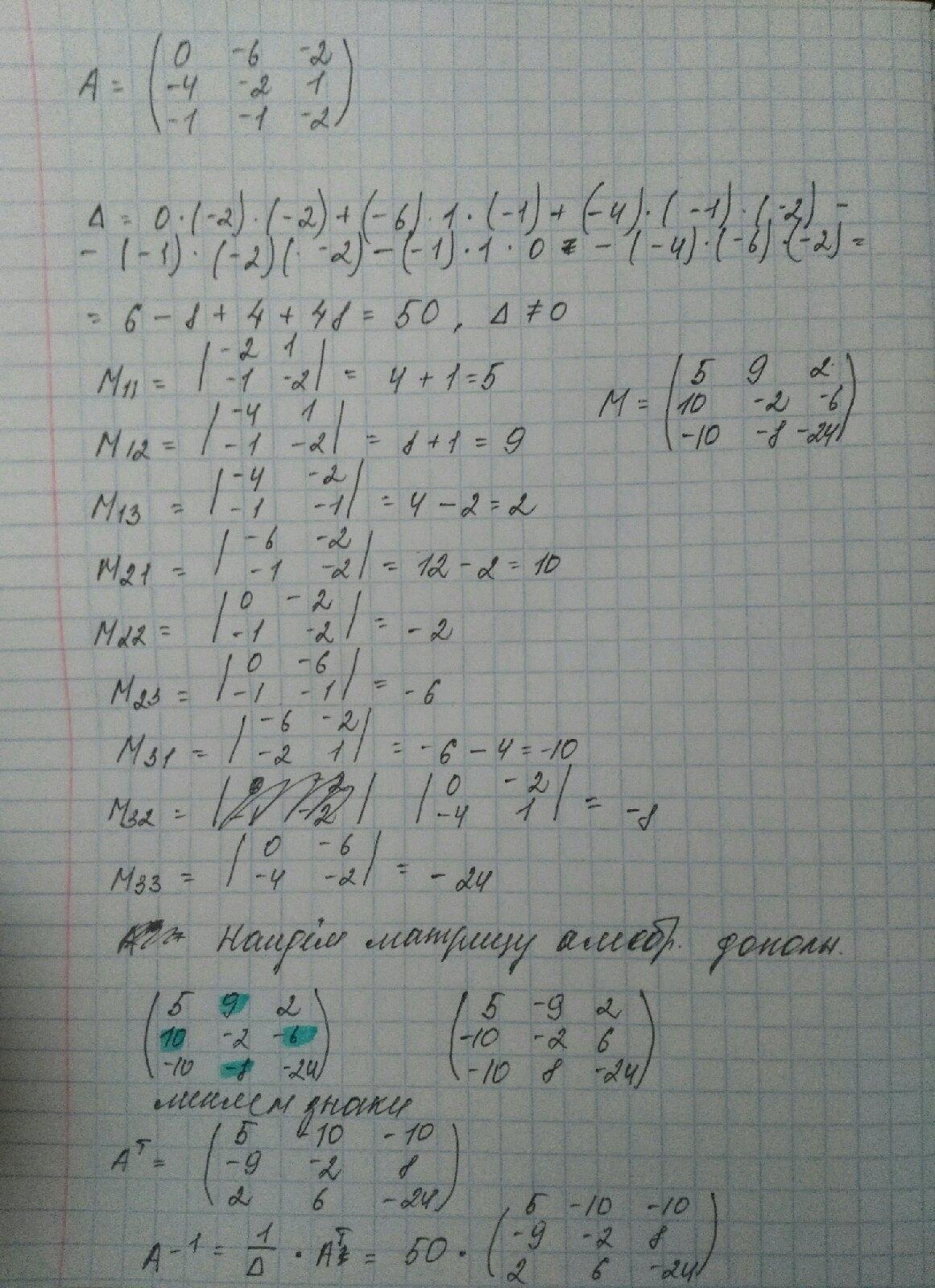
Автор ответа:
0
Ответ:
Проверка:
Похожие вопросы
Предмет: Русский язык,
автор: helenbuttrfly
Предмет: Қазақ тiлi,
автор: QueenRock
Предмет: Русский язык,
автор: 123456vlaD123456
Предмет: Математика,
автор: rukizhatdotdaeva
Предмет: Биология,
автор: Zvezda4689