помогите пожалуйста

Ответы
Ответ:
D)5
Объяснение:
Одна часть -а ,высота ВД делит АС на части 7 и 18 ⇒
АД=7а, ДС=18а ⇒ АС=25а.
Раз две равновеликие части , то S1=S2=S(ABC):2=(1\2*25а*6):2=37,5а
Отрезок х=КН ,К∈ВС, Н∈ДС ( параллельный высоте) отсекает на основании частицу у ( от точки С).х>0.
Площадь левой части ( до отрезках) состоит
S1=S(АВД)+S(тр).
37,5а=1\2*7а*6+S(тр).
16,5а=S(тр). Ищем высоту для трапеции.
ΔВСД≅ΔКСН по 2-м углам ⇒КН:ВД=СН:ДС , х:6=НС:18а , НС=3ха.
Высота трапеции ДН=18а-3ха=3а(6-х).
Все закидываем в 16,5а=S(тр).
1\2*(6+х)*3а*(6-х)=16,5а
6²-х²=33а:3а
36-х²=11
х²=25, х>0⇒ х=5
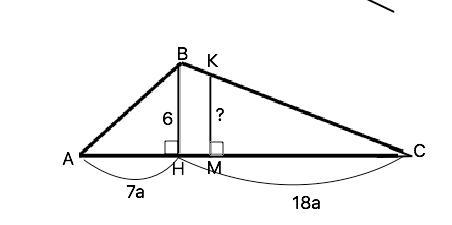
Высота треугольника равна 6, она делит основание на две части, относящиеся как 7:18. Найдите длину отрезка (прямой), параллельной высоте и делящей треугольник на равновеликие части.
Вариант решения.
Ответ: 5 (ед. длины)
Объяснение: Пусть дан ∆ АВС. его высота ВН=6, АН=7а, СН=18а, искомый отрезок КМ||ВН делит треугольник АВС на четырехугольник АВКМ и треугольник СКМ, площади которых равны.
Площадь АВС=ВН•АС/2=75а.
∆ СКМ и ∆ ВСН подобны по первому признаку подобия: КМ||ВН, прямая ВС - секущая => соответственные углы при В и К равны, угол С - общий.
Площадь ∆ ВСН=ВН•СН/2=6•18/2=54а
По условию площадь ∆ КСМ=КМ•СМ/2=Ѕ(АВС/2=37,5а
При этом Ѕ(ВСН):Ѕ(КСМ)=54а:37,5а=1,44
Отношение площадей подобных фигур равно квадрату коэффициента их подобия. => k=√1,44=1,2
Тогда ВН:КМ=1,2, откуда КМ=6:1,2=5 (ед. длины)
Если Ѕ(СКМ) равна половине Ѕ(АВС), то и Ѕ(АВКМ)=Ѕ(АВС):2, , т.е эти две части ∆ АВС равновелики, что и требовалось по условию.