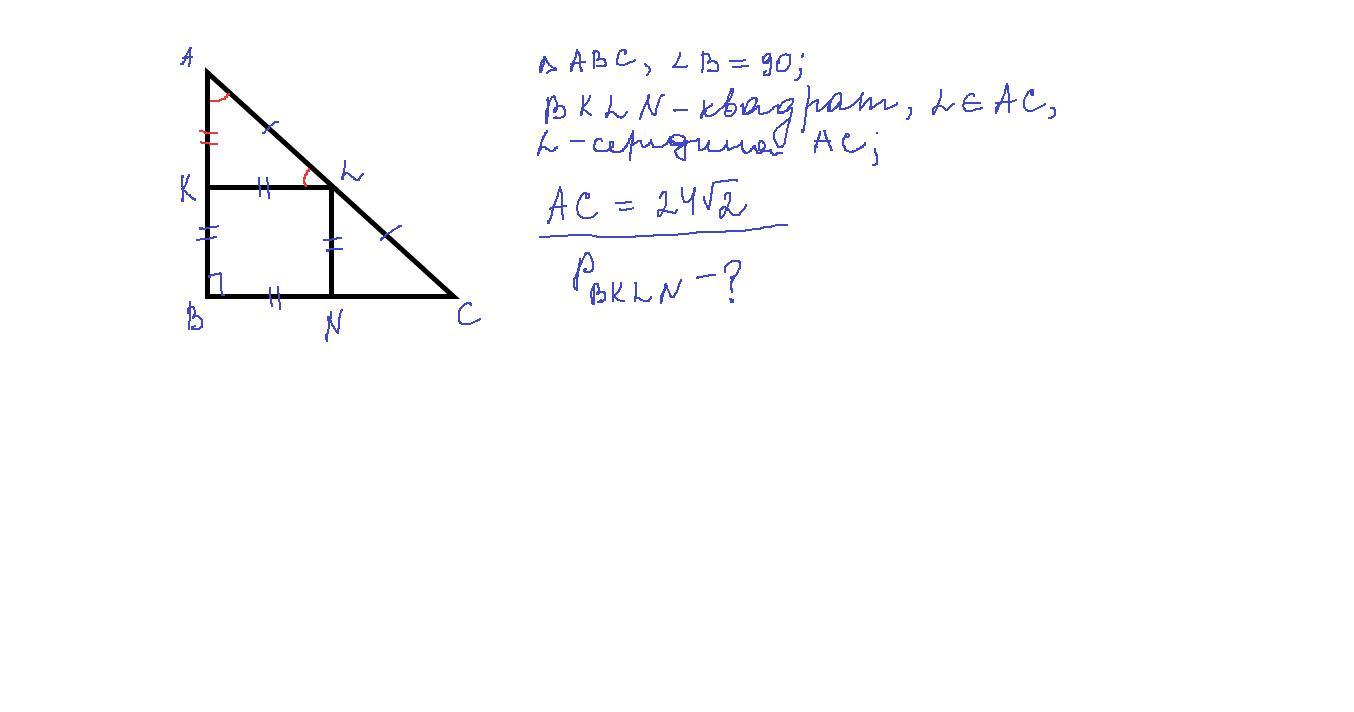
помогите пожалуйста

Ответы
Ответ: Р=48
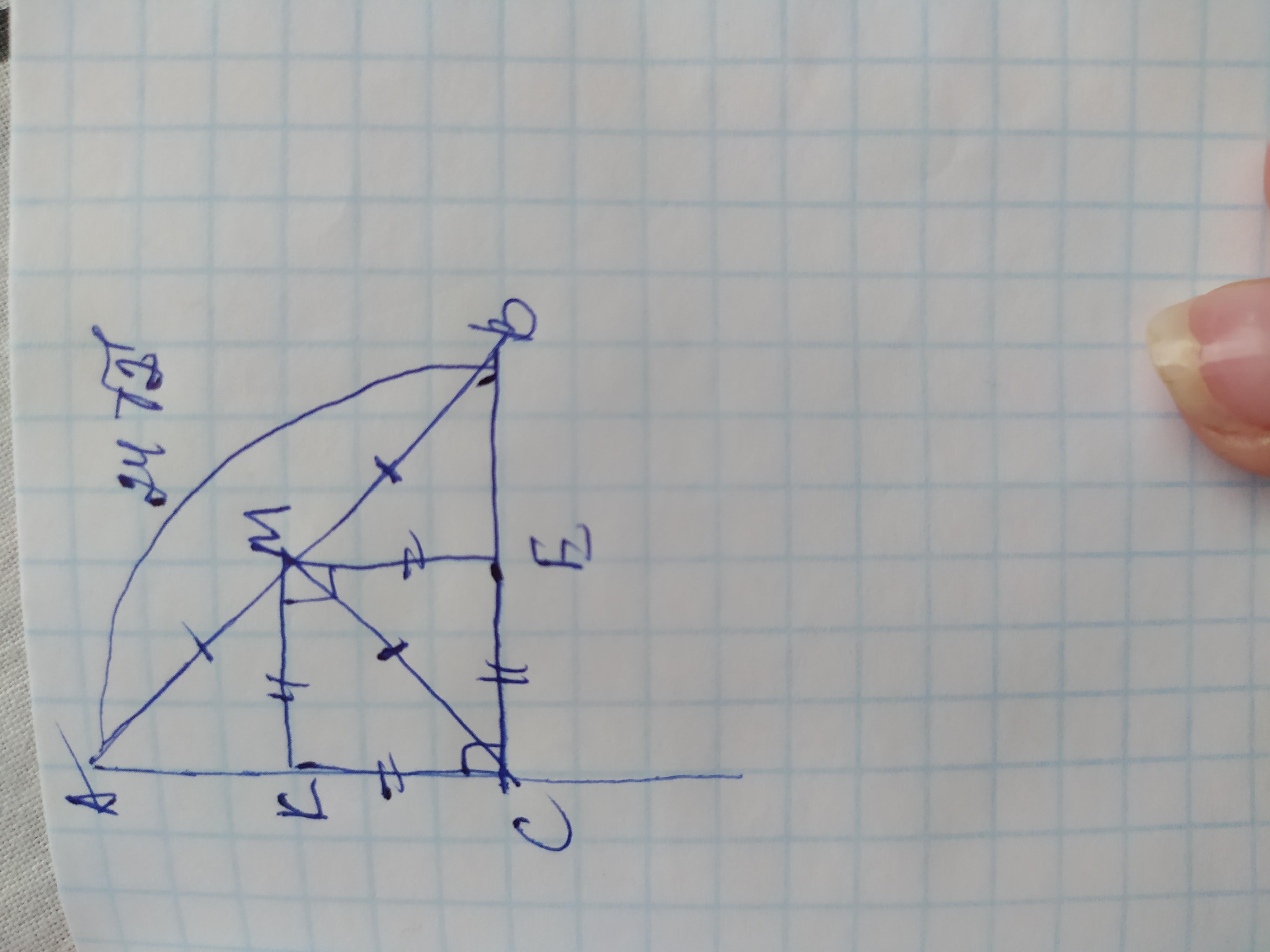
Объяснение: обозначим вершины треугольника А В С с прямым углом С и катетами АС и ВС и гипотенузой АВ. Три вершины квадрата обозначим КМЕ. Проведём диагональ квадрата СМ. Он является медианой так как АМ=ВМ=24√2/2=12√2. В прямоугольном треугольнике медиана проведённая из вершины прямого угла равна половине гипотенузы поэтому СМ=12√2
Диагональ СМ делит квадрат СКМЕ на 2 равных равнобедренных прямоугольных треугольника в которых стороны квадрата являются катетами а диагональ гипотенузой. В равнобедренном прямоугольном треугольнике катет меньше гипотенузы в √2 раз, поэтому
СК=КМ=МЕ=СЕ=12√2÷√2=12
Теперь найдём периметр квадрата зная его стороны: Р=12×4=48
1) KL║BC (т.к. KLNB - квадрат), L∈AC, AL=LC (т.к. L - середина АС), значит по теореме Фалеса (если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне) ВК=АК.
2) ΔАКL - прямоугольный равнобедренный с основанием АL, следовательно ∠КАL=∠АLК=45°.
3) AL=(1/2)*AC=(1/2)*24√2=12√2
4) В ΔAKL
sin<KAL=KL/AL
KL=sin<KAL*AL
KL=sin45*12√2
KL=(√2/2)*12√2
KL=12
5) P=4*KL=4-12=48
Ответ: В