Предмет: Алгебра,
автор: Jackoe89
Найти неопределённый интеграл на фото
Приложения:
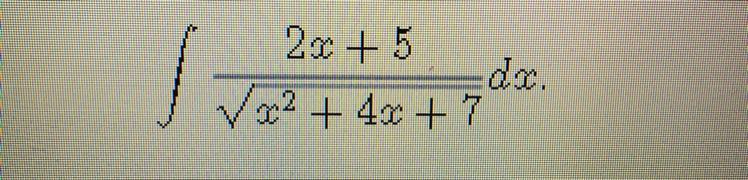
Ответы
Автор ответа:
2
Объяснение: см. во вложении
Приложения:

Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: totiq
Предмет: Русский язык,
автор: Khitarova
Предмет: Английский язык,
автор: len4ik1
Предмет: Математика,
автор: FlakSuper
Предмет: Математика,
автор: kiltek