Предмет: Алгебра,
автор: Cate213
Tb (V4 – 273 - 74 + 2V3)2 .
Вычислить корни на фотографии
Приложения:
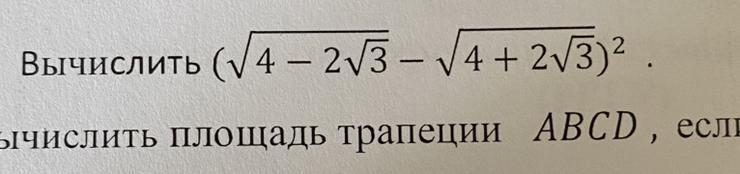
Ответы
Автор ответа:
2
Ответ:4
Решение:
Автор ответа:
1
Так как выражения внутри обеих модулей приобретают положительные значения, то оба модули раскроются с положительными знаками. Дальше имеем:
Ответ: 4
Похожие вопросы
Предмет: Русский язык,
автор: valentinavnik1
Предмет: Русский язык,
автор: vovanjr
Предмет: Русский язык,
автор: artem5420
Предмет: Математика,
автор: дженни34
Предмет: Геометрия,
автор: shusam