Question

Діагональ рівнобічної трапеції перпендикулярна до бічної сторони і є бісектрисою кута при основі.Знайти площу трапеції,якщо радіус описаного навколо неї кола дорівнює 40 см.

Answer 1

Ответ:

1200√3 см²

Объяснение:

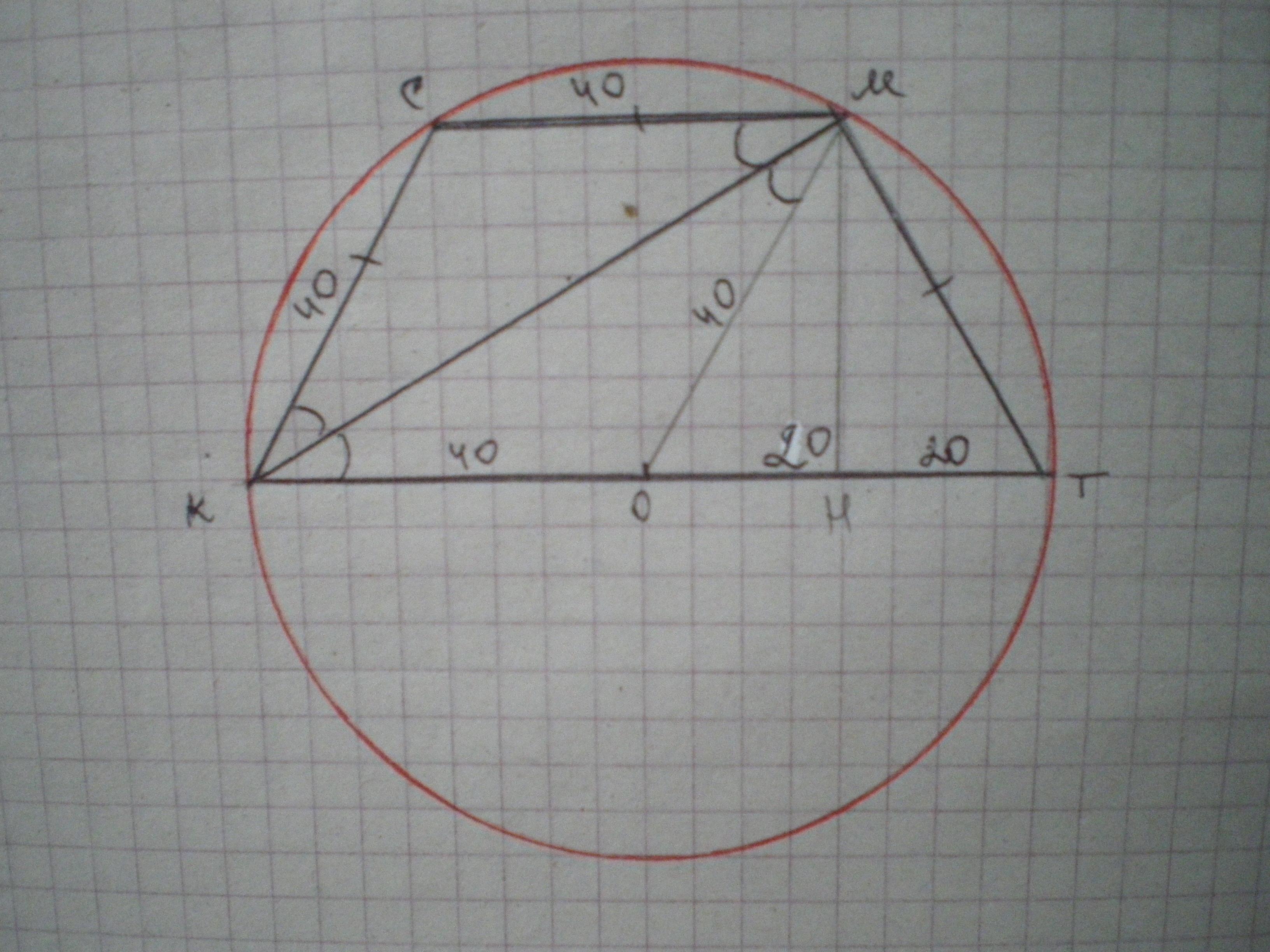
Дано: КСМТ - трапеція, КС=МТ, ∠КМТ=90°,  КМ - бісектриса, ОМ=КО=ОТ=40 см. Знайти S(КСМТ).

∠КМТ - прямий, отже він спирається на діаметр описаного кола, тоді КТ=КО+ОТ=80 см.

∠СКМ=∠ТКМ за умовою,  ∠СМК=∠ТКМ як внутрішні при СМ║КТ і січній КМ, отже ∠КСМ=∠СКМ, а ΔКСМ - рівнобедрений, КС=СМ.

Проведемо радіус ОМ=40 см, ΔКОМ=ΔКСМ за двома кутами і спільною стороною,  отже КС=СМ=КО=ОМ=40 см.

МТ=КС=40 см.

ΔОМТ - рівнобедрений, проведемо МН - висоту і медіану.

ОН=ТН=40:2=20 см

За теоремою Піфагора МН=√(МТ²-ТН²)=√(1600-400)=√1200=20√3 см.

S(КСМТ)=(СМ+КТ):2*МН=(40+80):2*20√3=1200√3 см²