ПОМОГИТЕ ПОЖАЛУЙСТА РАЗОБРАТЬСЯ 35 БАЛЛОВ
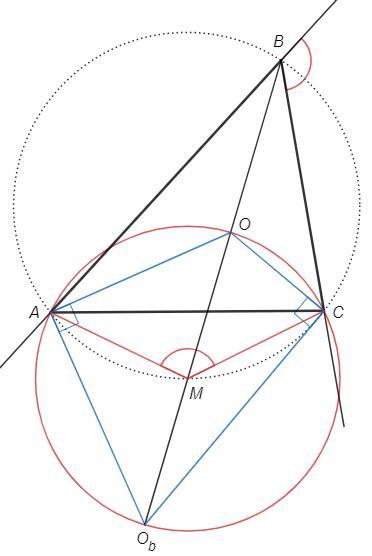
Продолжение биссектрисы угла B треугольника ABC пересекает описанную окружность в точке M; O — центр вписанной окружности, Ob — центр вневписанной окружности, касающейся стороны AC. Докажите, что точки A, C, O и Ob лежат на окружности с центром M.
Ответы
Центр вписанной окружности (O) - пересечение биссектрис внутренних углов.
Центр вневписанной окружности (Ob) - пересечение биссектрис внешних углов.
Поскольку центр Ob лежит на биссектрисах внешних углов A и С, он равноудален от прямых AB, AC, BC, следовательно лежит на биссектрисе угла B.
Биссектрисы внешнего и внутреннего углов перпендикулярны (сумма смежных углов 180, сумма их половин 90).
В четырехугольнике AOCOb противоположные углы прямые (сумма 180), следовательно он вписанный, OOb - диаметр.
Пусть M - середина OOb, центр описанной окружности AOCOb.
AMC =∪AO+∪CO =2ACO +2CAO =A+C
В четырехугольнике ABCM внешний угол равен внутреннему при противолежащей вершине, следовательно четырехугольник вписанный.
То есть M лежит на описанной окружности ABC.