Предмет: Математика,
автор: kokosaun
Знайти частинний розв’язок рівняння:По можливостi Зробiть розв'язання в зошитi
Приложения:
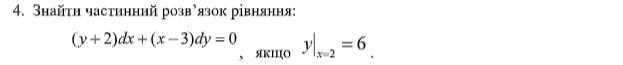
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Дифференциальное уравнение с разделяющимися переменными
Задача Коши:
Автор ответа:
0
разделим переменные dy/(y+2)=-dx/(x-3)⇒㏑Iy+2I=-㏑Ix-3I+㏑IcI; c≠0;
у=с/(х-3)-2
используя нач. данные, найдем частное решение. 6=(с/(2-3))-2⇒с=-8
у=-2-(8/(х-3))
у=-(2х+2)/(х-3)
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Русский язык,
автор: Dykyryyy
Предмет: Українська мова,
автор: Аноним
Предмет: Геометрия,
автор: qwertyuiophjkhg
Предмет: Математика,
автор: диман500