Предмет: Математика,
автор: frager90
Исследовать ряды на сходимость
Приложения:
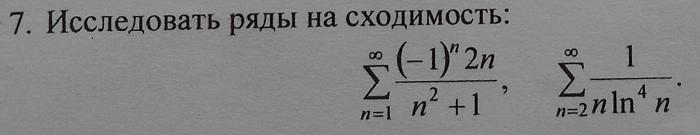
Ответы
Автор ответа:
0
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
По второму признаку Лейбница предел ряда должен стремится к 0.
Таким образом, рассматриваемый ряд сходится. Теперь нужно исследовать на абсолютной и условной сходимости ряда. Возьмём данный ряд по модулю
- расходящийся ряд, поскольку
- гармонический ряд расходится. Следовательно, данный ряд сходится условно.
По интегральному признаку:
Несобственный интеграл сходится, а значит сходится и рассматриваемый ряд
Похожие вопросы
Предмет: Английский язык,
автор: dedushkaRuslan
Предмет: Русский язык,
автор: Валерия27062006
Предмет: Русский язык,
автор: dashadenize
Предмет: Химия,
автор: trash15
Предмет: Химия,
автор: lotarevar