Предмет: Математика,
автор: dbazhenov2002
Вычислить интеграл..
Приложения:
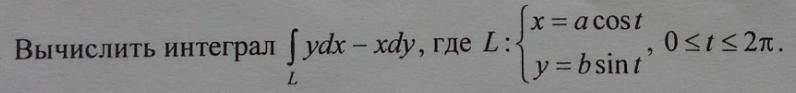
Ответы
Автор ответа:
0
Немного не уверен
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: LevzenkoMargari
Предмет: Русский язык,
автор: karolina13
Предмет: Русский язык,
автор: perizat1383
Предмет: Химия,
автор: SugaYoongi1508