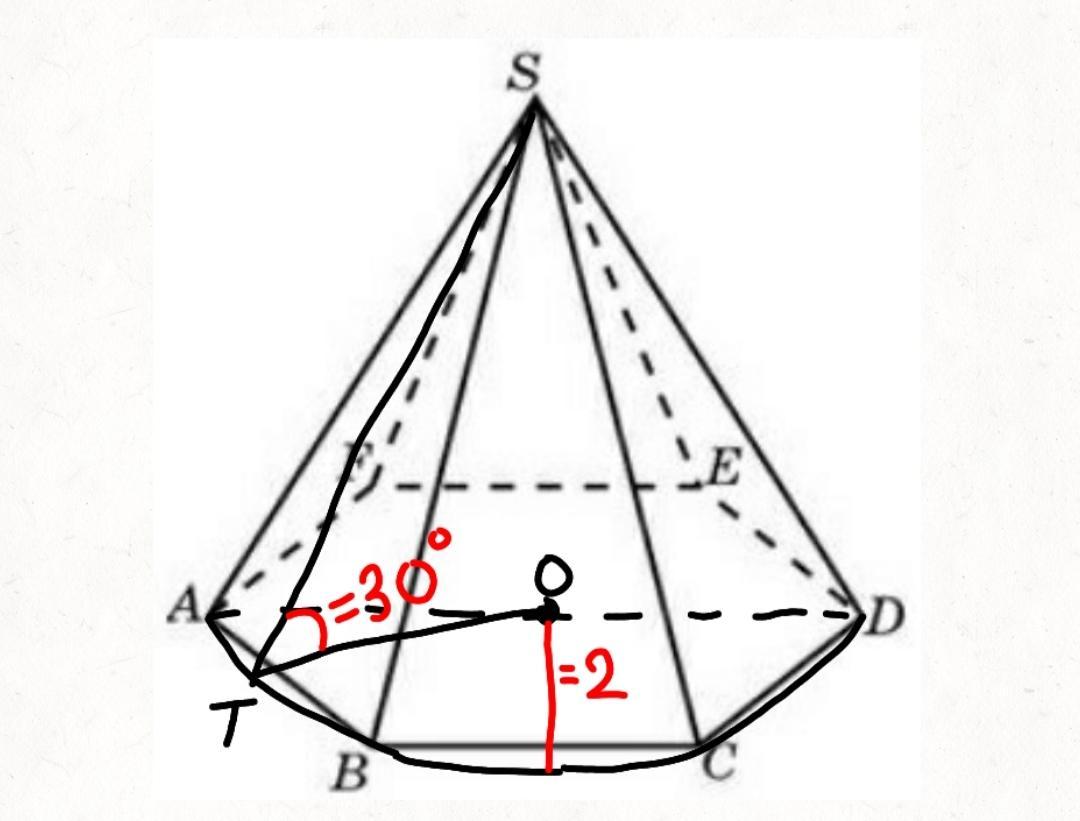
ПОМОГИТЕ ЗНАТОКИ!!! В правильной шестиугольной пирамиде радиус окружности, описанной вокруг основания равен 2, а угол между боковой гранью плоскостью основания равен 30°. Найдите площадь боковой поверхности пирамиды. (Формула для нахождения: S=1/2Ph)
Ответы
Ответ:
12 см²
Объяснение:
Шестиугольник образован из 6 равносторонних треугольников сторона треугольника равна радиусу.
а=R=2 cm
Найдем высоту треугольника по формуле
h=а√3/2
h=2√3/2=√3 высота треугольника
Найдем апофему пирамиды.
cos30°=h/H
cos30°=√3/2
√3/2=√3/H
H=2√3/√3
H=2cm апофема пирамиды.
Р=6*а=6*2=12 см периметр шестиугольника
S=1/2РH=1/2*12*2=12 см² площадь боковой поверхности пирамиды
Ответ:
Объяснение:
Сторона правильного шестиугольника равна радиусу описанной окружности. Следовательно сторона а основания равна 2 ед. Боковая сторона правильной шестиугольной пирамиды состоит из шести равнобедренных треугольников с основанием а=2. Проведем высоту в основании и найдем её по т.Пифагора. h=√(2²-1²)=√3 ед. Плоскость боковой стороны наклонена под углом 30°, следовательно угол между высотой пирамиды и высотой боковой грани - 30°. Высота пирамиды, высота грани и высота треугольника основания - прямоугольный треугольник с гипотенузой - высота боковой грани и катетами - высота пирамиды - Н и высота треугольника основания - √3. По свойству катета лежащего против угла 30° составляем уравнение:
(2Н)²=(√3)²+Н², где Н - высота пирамиды;
3Н²=3
Н=1 ед;
тогда апофема равна - 2Н=2 ед;
Р=6*2=12 ед;
S=12*2*1/2=12 ед².