Question

9. В треугольнике ABC. BD-медиана. АВ=2см,
ВС- 2✓2 см, угол CBD-30°. Найти угол ABC.​

Answer 1

Ответ:

∠ABC = 75°

Объяснение:

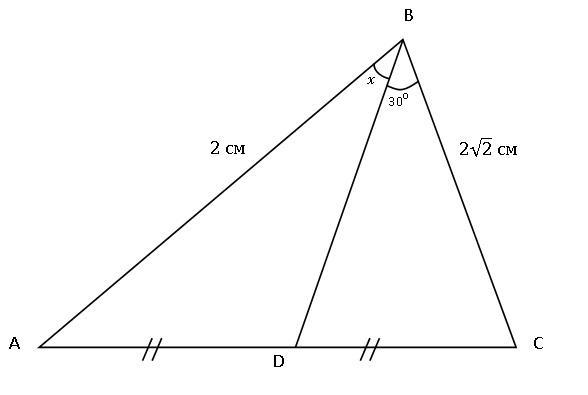
Дано: ΔABC, AB = 2 см, BC = 2√2 см, BD медиана, ∠CBD = 30°.

Найти ∠ABC.

Решение.

Обозначим для удобства ∠ABD через x.

Медиана делит треугольник на два равновеликих треугольника, т.е на два треугольника с равными площадями.

S₁ (ΔABD) = S₂ (ΔDBC)

$S_{1} = \frac{1}{2} AB*BD*sin x = \frac{1}{2} *2*BD*sinx=BD*sinx$

$S_{2} =\frac{1}{2} *BC*BD*sin 30^{0} =\frac{1}{2} *2\sqrt{2} *BD*\frac{1}{2} =BD*\frac{\sqrt{2}}{2}$

$BD*sinx=\frac{\sqrt{2}}{2} *BD\\\\sinx=\frac{\sqrt{2} }{2}$

$x=45^{0}$, ∠ABD = 45°

∠ABC = ∠ABD  + ∠DBC = 45° + 30° = 75°