Question

Доведіть, що в опуклому чотирикутнику сума діагоналей менша від
периметра.​

Answer 1

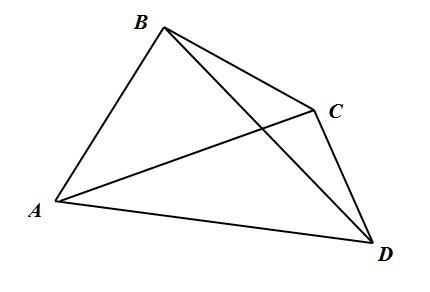
Пусть ABCD - выпуклый четырехугольник с диагоналями AC и BD. Докажем, что AC + BD < P₄.

Воспользуемся неравенством треугольника: в треугольника любая сторона меньше двух других.

В ΔABС AC < AB + BC,

В ΔACD AC < AD + CD,

В ΔBCD BD < BC + CD,

В ΔABD BD < AB + AD.

Почленно сложим все четыре неравенства:

2AC + 2BD < 2AB + 2BC + 2AD + 2CD | : 2

AC + BD < AB + BC + CD + AD = P₄, что и требовалось доказать.