Предмет: Алгебра,
автор: Ифигения
Задана функция f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
Приложения:
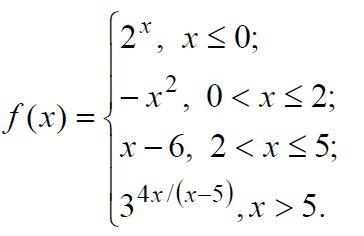
Ответы
Автор ответа:
3
Ответ:
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
При х=0 функция имеет разрыв 1 рода .
При х=2 функция непрерывна.
При х=5 функция имеет разрыв 2 рода .
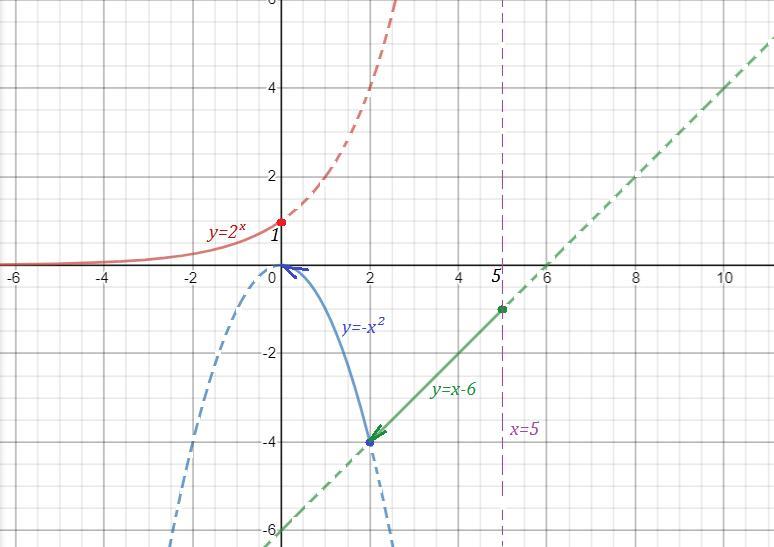
График функции нарисован сплошной линией.
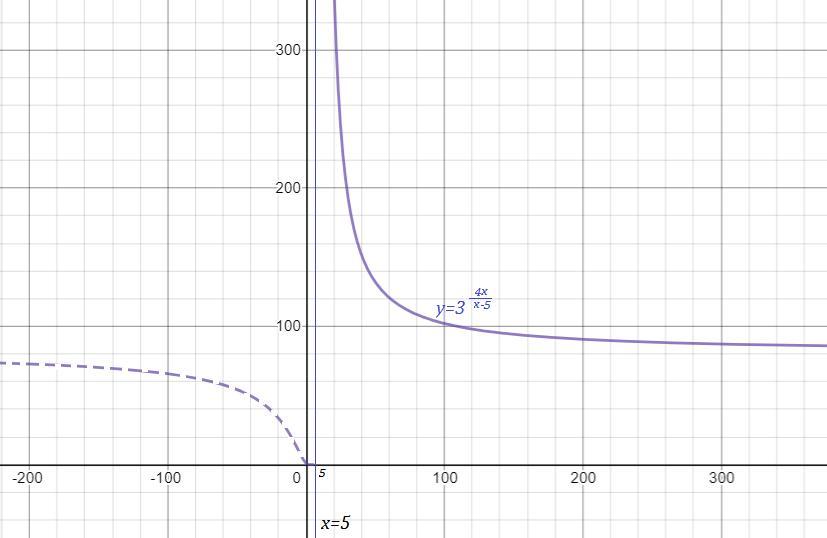
На 1 рисунке нет чертежа функции при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
Приложения:
Ифигения:
Большое спасибо! С чертежом сама управлюсь! Не могли бы вы глянуть, пожалуйста, задание наподобие этого? https://znanija.com/task/37787222
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: rekhtinaPolina
Предмет: Другие предметы,
автор: camper1973
Предмет: Алгебра,
автор: Софа3011
Предмет: Литература,
автор: прррррл1