Question

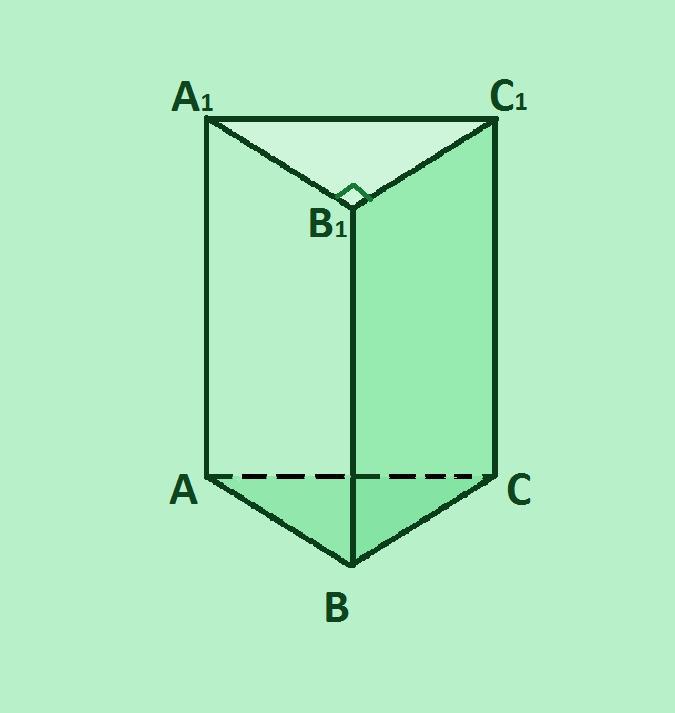
Основание прямой призмы – прямоугольный треугольник с гипотенузой 10 см и катетом 6 см. Боковое ребро призмы равно 7 см. Найдите. площадь полной поверхности призмы. Выполните рисунок.
Заранее спасибо!

Answer 1

Ответ:

S=216 sm²

Пошаговое объяснение:

Если основание призмы

прямоугольный треугольник

с гипотенузой 10 см и катетом 6 см, то

другой катет равен на 8 см

$\sqrt{10^2-6^2 } =\sqrt{100-36}=\sqrt{64} =8$

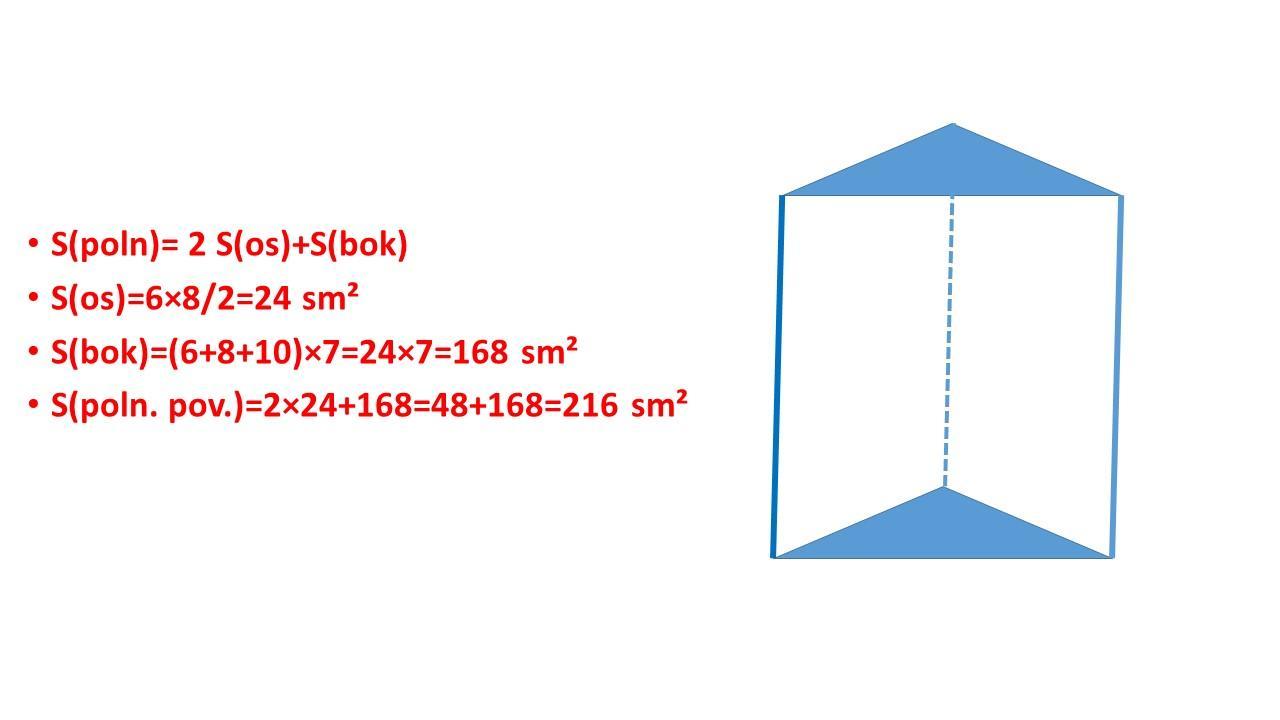
S(poln)= 2 S(os)+S(bok)

S(os)=6×8/2=24 sm²

S(bok)=(6+8+10)×7=24×7=168 sm²

S(poln. pov.)=2×24+168=48+168=216 sm²

Answer 2

Ответ:

Sпов=216 кв.см.

Пошаговое объяснение:

Дано:

Прямая призма со сторонами:

AC=10 см; AB=6 см; BB1=CC1=AA1=7 см.

Найти: Sпов-?

Решение:

По теореме Пифагора:

1) BC=$\sqrt{AC^{2} -AB^{2} }=\sqrt{10^{2}-6^{2} } =\sqrt{64} =8$ см

Треугольники в верхнем и нижнем основании равны. Значит и площади этих треугольников равны. Найдём площадь треугольника в оснований:

2)Sabc=Sa1b1c1=$\frac{h*AB}{2}$=$\frac{BC*AB}{2}$=$\frac{8*6}{2} =24$ кв.см.

Боковые грани призмы представляют собой прямоугольники, поэтому вычисляем площадь каждого прямоугольника:

3) Sbb1c1c=BB1*BC=7*8=56 кв.см.

4) Sa1ab1b=AA1*AB=7*6=42 кв.см.

5) Saa1c1c=AA1*AC=7*10=70 кв.см.

Площадь поверхности призмы:

Sпов=Sabc+Sa1b1c1+Sbb1c1c+Sa1ab1b+Saa1c1c=24+24+56+42+70=216 кв.см.