Предмет: Алгебра,
автор: Alita567
Вычислить двойной интеграл по области , ограниченной указанными линиями.
Приложения:
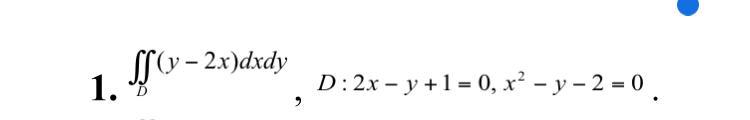
Ответы
Автор ответа:
2
Приложения:
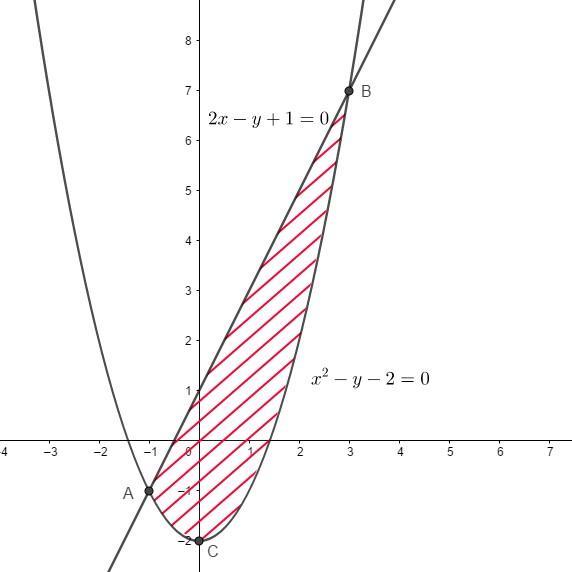
Simba2017:
вопрос можно?
Какой?
почему нижний предел второго интеграла не x^2-2?
Выражаем через y уравнение x^2-y-2=0, т.е. y = x^2-2
Ну опечатался вместо 2
Сейчас исправлю
давайте исправьте , я думаю не одна я такие решения в свою кубышку собираю)))))))))
Готово.
и ответ красивый, спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: kaledich96
Предмет: Русский язык,
автор: zaqwsx1
Предмет: Русский язык,
автор: 20kuyan
Предмет: История,
автор: elena27gr
Предмет: Математика,
автор: Аноним