Предмет: Математика,
автор: alinashlyushin
срочно ! решить несобственный интеграл или доказать его расходимость
Приложения:
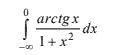
Ответы
Автор ответа:
0
, а значит точка 0 не особая. Тогда единственная особая точка
.
Похожие вопросы
Предмет: Английский язык,
автор: aap02
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: kexifz09
Предмет: Литература,
автор: мяу177
Предмет: Алгебра,
автор: Vados2002k