Предмет: Алгебра,
автор: qnarikpoghosyan16

Найти f'(x) =0
Simba2017:
по-моему не существует, на 0 делить нельзя
нет, существует, - 1/4
что тогда спрашиваете?
я знаю ответ, решение не знаю ♀️
Ответы
Автор ответа:
1
Объяснение:
так как х под корнем с -, то можно с самого начала дописать, что x<=0
Приложения:
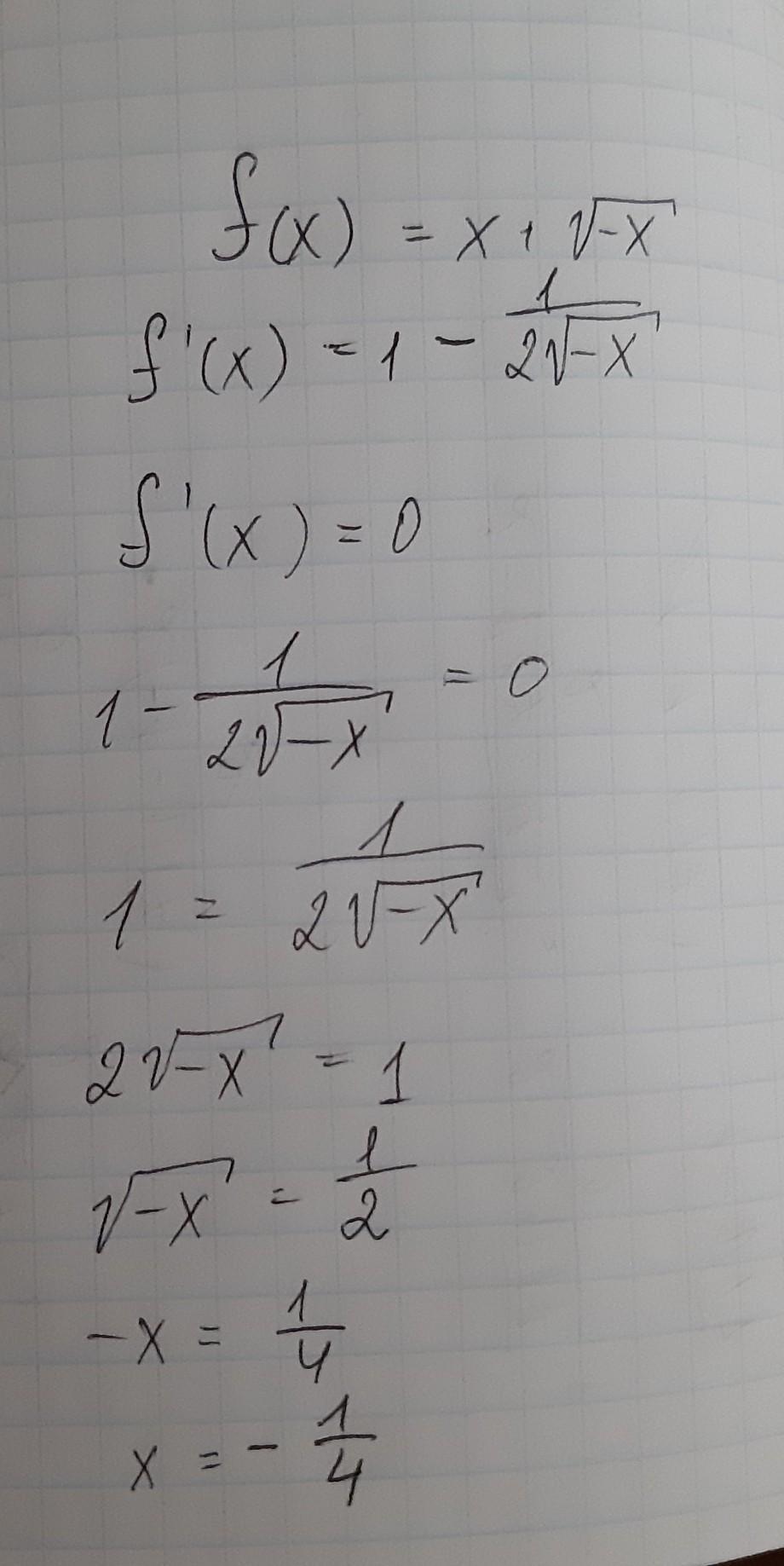
Автор ответа:
2
Объяснение:
f'(x) =
f'(x) = 0:
Похожие вопросы
Предмет: Английский язык,
автор: sergunkina97
Предмет: Українська література,
автор: evgeniisorok
Предмет: Русский язык,
автор: narekmariam1996
Предмет: Математика,
автор: крутой274
Предмет: Литература,
автор: Lyubov261