Question

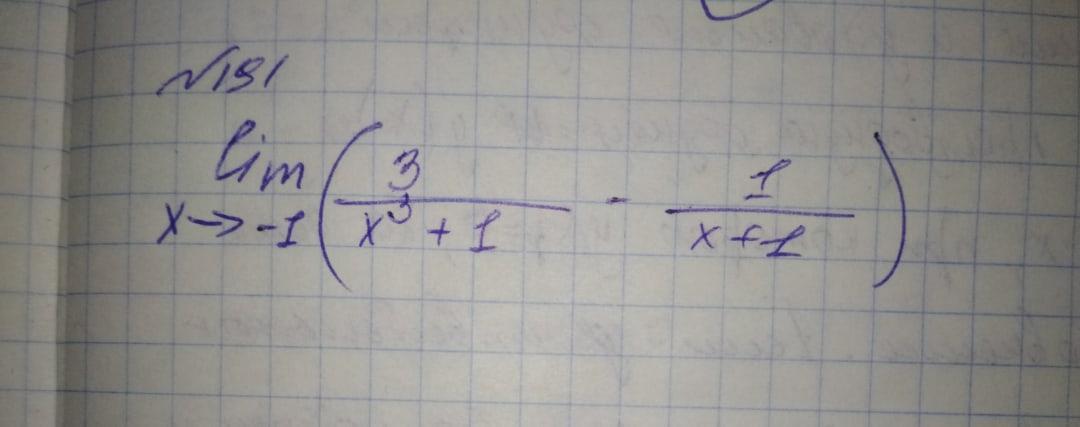
Помогите найти предел тригонометрической функции (пустое решение без объяснений не нужно, жду объяснения для чайников) (задание во вложении)

Answer 1

$\displaystyle\\ \lim_{x \to -1} \bigg( \frac{3}{x^3+1}-\frac{1}{x+1} \bigg)=\frac{3}{(-1)^3+1}-\frac{1}{-1+1}=\frac{3}{0}-\frac{1}{0}\\\\\\\lim_{x \to -1}\bigg(\frac{3}{(x+1)(x^2-x+1)}-\frac{1}{x+1}\bigg)=\lim_{x \to -1} \frac{3-(x^2-x+1)}{(x+1)(x^2-x+1)}=\\\\\\\\=\lim_{x \to -1} \frac{3-x^2+x-1}{x^3-x^2+x+x^2-x+1}=\lim_{x \to -1} \frac{-x^2+x+2}{x^3+1}= \lim_{x \to -1} \frac{(-x^2+x+2)'}{(x^3+1)'}=\\\\\\=\lim_{x \to -1} \frac{-2x+1}{3x^2}=\frac{-2*(-1)+1}{3*(-1)^2}=\frac{2+1}{3}=\frac{3}{3}=1$

Answer 2

(3-(x^2-x+1))/(x^3+1)=(-x^2+x+2)/(x^3+1)=-(x-2)(x+1)/((x+1)(x^2-x+1)=

=(2-x)/(x^2-x+1)

lim(2-x)/(x^2-x+1)=(2-(-1))/(1+1+1)=3/3=1