Предмет: Геометрия,
автор: soloninkamaria
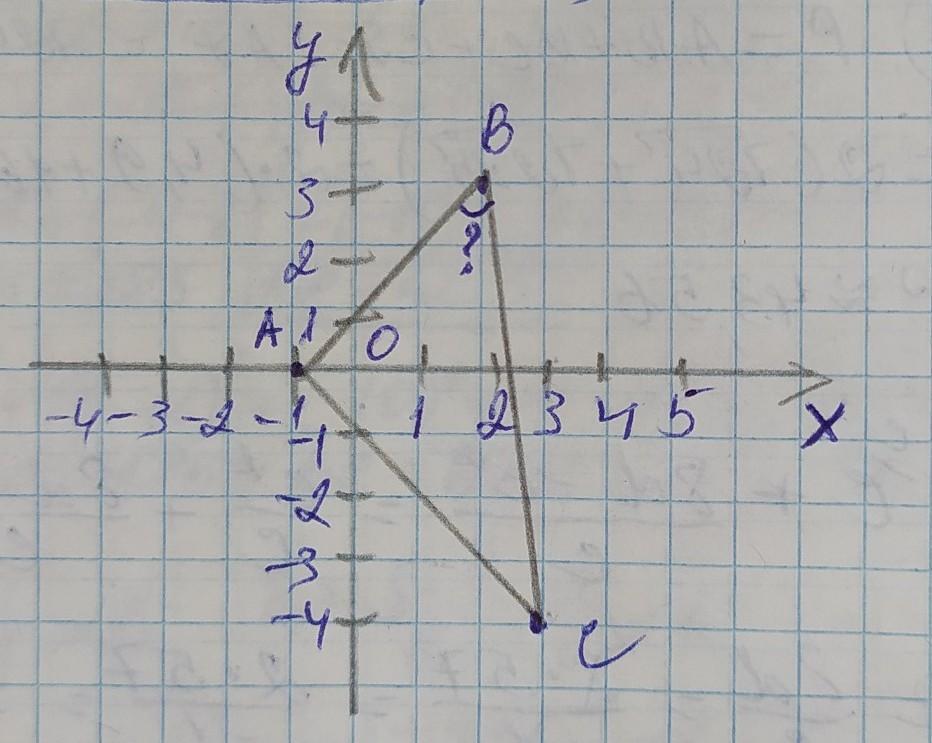
знайдіть косинус кута В трикутника АВС, якщо А(-1;0) В(2:3), С(3;-4)
Ответы
Автор ответа:
6
Відповідь:
cosB= 0,6
Знайдіть косинус ∠В трикутника АВС, якщо
А(-1; 0) В(2; 3), С(3; -4)
РІШЕННЯ:
∠В знаходиться між сторонами трикутника ВА і ВС, знайдемо координати ціх сторін за формулою:
ВА (Хa–Xb; Ya–Yb)=(–1–2; 0–3)=(–3; –3)
ВС (Xc–Xb; Yc–Yb)=(3–2; –4–3)=(1; –7)
ВА (–3; –3);
ВС (1; –7).
Знайдемо косинус ∠В за формулою:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: veronikashkurapey
Предмет: Английский язык,
автор: dan4s
Предмет: Русский язык,
автор: marusenkaivanova
Предмет: Алгебра,
автор: макс1236662
Предмет: Алгебра,
автор: ghgvh3