Предмет: Алгебра,
автор: alenaalenaproshina55
ПОМОГИТЕ СРОЧНО!!!! ЗАРАНЕЕ СПАСИБКИ ))
Приложения:
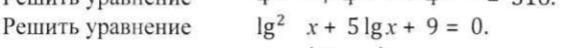
prokhpav:
Почему никто не решает квадратные уравнения с отрицательным дискриминантом? Получилась вполне себе вменяемая комплексная степень, для экзамена самое то
Я в подтверждение забил уравнение в онлайн калькуляторе, и прикрепил обрезанный скриншот. Но там-то нет подробного решения, я сам это всё решил
Я просто быстро печатаю и пользуюсь ctrl-c ctrl-v
"Напишите ей сообщение с вопросом о удалении" - как?
А, всё, нашел где
Ответы
Автор ответа:
1
Ответ:
Объяснение:
x>0
пусть lg(x)=t, тогда
t²+5t+9=0
D= 25-36= -11
D<0 => корней нет
Автор ответа:
1
На случай, если кому-то нужно решение в комплексных числах
Похожие вопросы
Предмет: Английский язык,
автор: Cartman6
Предмет: Русский язык,
автор: Irichaprivalova
Предмет: Русский язык,
автор: guzovvova
Предмет: Физика,
автор: zakatalibli