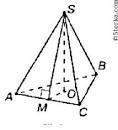
Сторона основания правильной треугольной пирамиды равна 4 см.боковая грань наклонена к плоскости основания под углом 60 градусов. Найти объем пирамиды Поможете?)
Ответы
Ответ:
Пошаговое объяснение:
V=1\3*S*h.
S(основ)=а²√3\4⇒ S(основ)=16√3\4=4√3 см²
В правильном ΔАВС( основание пирамиды) высоты,медианы пересекаются в одной тоске О-центре основания.Пусть АМ-высота . Высота основания √(16-4)=2√2 см. Медианы делятся 2:1 считая от вершины ,ОМ=2√2\3 см.
Из ΔРОМ : tg60=h\OM , h=2√(2\3).
V=1\3*4√3*2√(2\3)=8√2\3 см³
Ответ:8√3/3
Пошаговое объяснение:Объем пирамиды равен одной трети произведения площади основания на высоту: где S – площадь основания, H – высота пирамиды.
1) У нас: S=a²√3/4 = 4²·√3/4=4√3 2)Найдём радиус вписанной окружности в треугольник r=OM из формулы: S=p·r, где р-полупериметр; р=(4+4+4):2=6; r= S/p= 4√3/6=2√3/3; 3)Тогда высота пирамиды из ΔSOM: SO=H= r·tg60°= 2√3/3 · √3= 2 4) V=1/3 ·S ·H ⇒ V= (1/3)·4√3 ·2=8√3/3