Предмет: Алгебра,
автор: lyntikkkkkk
Сложите квадратное уравнение с целыми коэффициентами, корни которого равны -1/5 и 5! Буду благодарна))
Ответы
Автор ответа:
1
Объяснение:
Запишем теорему Виетта.
здесь нужно найти целые решения второго уравнения. для первого их легко найти
искомое уравнение это
Изменено: второе уравнение имеет бесконечно много решений. Поэтому их можно легко найти подбором
dnepr1:
Искомое уравнение неверно найдено - оно не даёт заданные корни. Правильный ответ: 5x^2-24x-5=0.
Ошибка в сумме корней: не 5,2, а (24/5).
Автор ответа:
0
Ответ: х^2-4,8*х-1.
Объяснение:
Приложения:
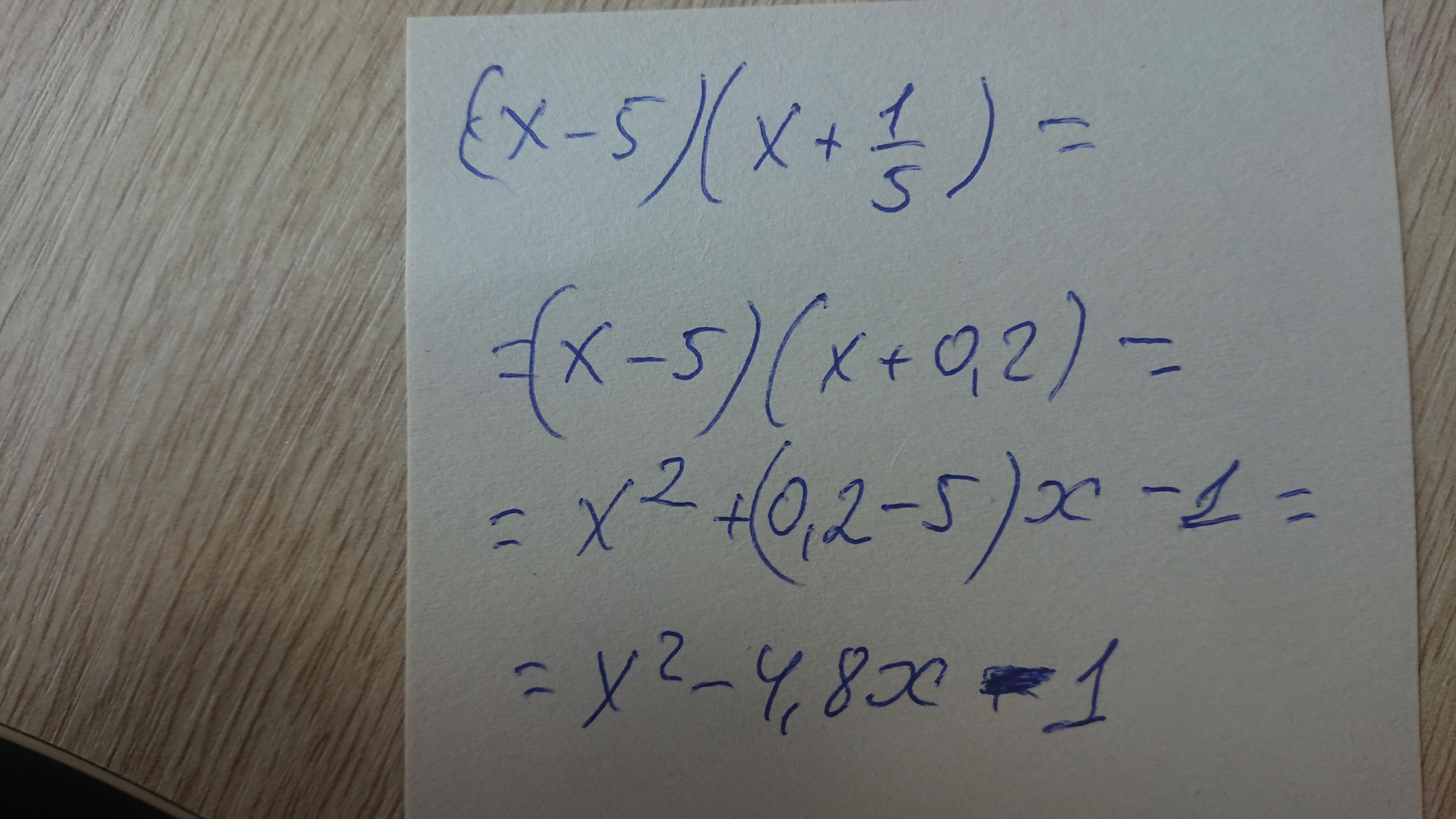
многочлен с целыми коэфицэнтами! У вас с дробными
Похожие вопросы
Предмет: Русский язык,
автор: gila55
Предмет: Другие предметы,
автор: Лейла13000000000
Предмет: Русский язык,
автор: арина0405
Предмет: Литература,
автор: василийко1
Предмет: Биология,
автор: Zaalina03