Найти корни уравнения.
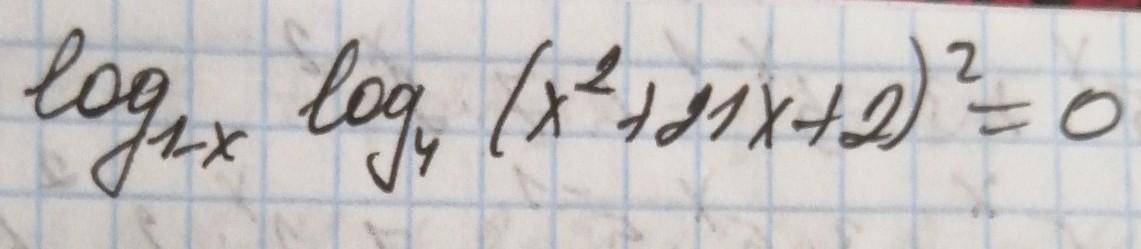
Ответы
log(1-x) (log(4)(x^2 + 21x + 2)^2) = 0
одз
1 - x > 0 x < 1
1 - x ≠ 1 x ≠ 0
(x^2 + 21x + 2)^2 > 0
x^2 + 21x + 2 ≠ 0 D = 21^2 - 8 = 433 x12 ≠ (-21 +- √433)/2
log(4)(x^2 + 21x + 2)^2 > 0 (x^2 + 21x + 2)^2 > 1
(x^2 + 21x + 2)^2 - 1 > 0
(x^2 + 21x + 1)(x^2 + 21x + 3) > 0
D= 441 - 4 = 437 x12 = (-21 +- √437)/2
D = 441 - 12 = 429 x34 = (-21 +- √429)/2
+++++(-21 - √437)/2 --------- (-21 - √429)/2 ++++ (-21 + √429)/2 ------ (-21 + √437)/2 ++++++++
x∈(-∞, (-21 - √437)/2) U ((-21 - √429)/2,(-21 +√429)/2) U ((-21 +√437)/2, 0) U (0, 1)
log(1-x) (log(4)(x^2 + 21x + 2)^2) = 0
log(4)(x^2 + 21x + 2)^2 = 1
(x^2 + 21x + 2)^2 = 4
(x^2 + 21x + 2)^2 - 2^2 = 0
(x^2 + 21x+ 2 - 2)(x^2 + 21x + 2 + 2) = 0
(x^2 + 21x)(x^2 + 21x + 4) = 0
x(x + 21)(x^2 + 21x + 4) = 0
x = 0 нет по одз
x = -21
вторая скобка
D = 21^2 - 4*4 = 441 - 16 = 425
x12 = (-21 +- √425)/2
√425 = 5√17 x12 = (-21 +- 5√17)/2
ответ x12 = (-21 +- 5√17)/2 х3=-21
(x^2 + 21x)(x^2 + 21x + 4)