Предмет: Алгебра,
автор: purple14wok88
преобразовать выражение,как можно подробнее
Приложения:
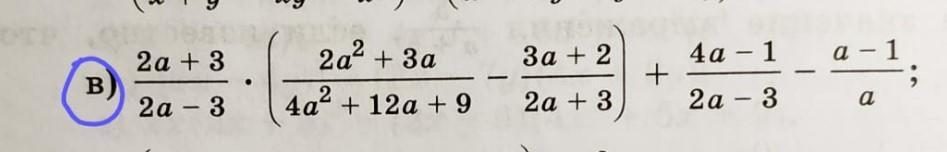
Ответы
Автор ответа:
1
Ответ:
1/а.
Объяснение:
Преобразовать (упростить):
[(2a+3)/(2a-3)]*[(2a²+3a)/(4a²+12a+9)]-[(3a+2)/(2a+3)]+[(4a-1)/(2a-3)]-[(a-1)/a];
1)В скобках. Преобразовать:
числитель первой дроби:(2a²+3a)=а(2а+3);
знаменатель первой дроби:(4a²+12a+9)=(2а+3)²;
Вычитание:
[а(2а+3)/(2а+3)²] - [(3a+2)/(2a+3)]=
сокращение на (2а+3) в первой дроби:
=[а/(2а+3)] - [(3a+2)/(2a+3)]=
общий знаменатель (2a+3):
=(а-3а-2)/(2а+3)=
=(-2а-2)/(2а+3);
2)Умножение:
[(2a+3)/(2a-3)] * [(-2а-2)/(2а+3)]=
=[(2a+3)*(-2a-2)] / [(2а-3)*(2а+3)]=
сокращение на (2а+3) в числителе и знаменателе:
=(-2a-2)/(2а-3);
3)Сложение:
[(-2a-2)/(2а-3)] + [(4a-1)/(2a-3)]=
общий знаменатель (2а-3):
=(-2а-2+4а-1)/(2а-3)=
=(2а-3)/(2а-3)=1;
4)Вычитание:
1-[(а-1)/а]=
общий знаменатель а:
=(a-a+1)/a=
=1/a.
Похожие вопросы
Предмет: Другие предметы,
автор: анастасия200003
Предмет: Английский язык,
автор: елизаветадущ
Предмет: Русский язык,
автор: УльянаБеспалова546
Предмет: Физика,
автор: javoxirbek