Предмет: Математика,
автор: NikitaVologin
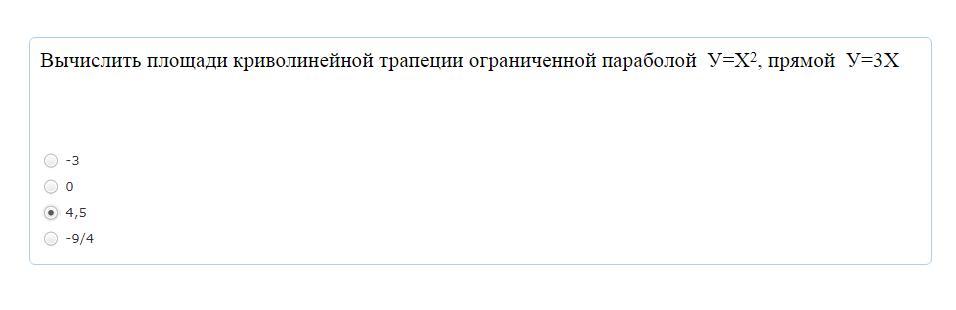
Вычислить площадь криволинейной трапеции
Приложения:
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
у₁ = 3х
у₂ = х²
найдем точки пересечения графиков
х²= 3х; х²-3х = 0; х(х-3) = 0; х₁ = 0; х₂ = 3
теперь посчитаем интеграл
ответ 4,5
Похожие вопросы
Предмет: Русский язык,
автор: s2804
Предмет: Русский язык,
автор: oksana12112006
Предмет: Русский язык,
автор: hazaragaev
Предмет: Биология,
автор: nana77777771
Предмет: Математика,
автор: avchargrisha