Предмет: Математика,
автор: sofyaglebowa
СРОЧНО Решите уравнение: В ответ запишите количество корней, принадлежащих отрезку ![[-\frac{\pi }{2}, 2\pi] [-\frac{\pi }{2}, 2\pi]](https://tex.z-dn.net/?f=%5B-%5Cfrac%7B%5Cpi+%7D%7B2%7D%2C+2%5Cpi%5D)
Приложения:
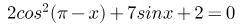
Ответы
Автор ответа:
1
Замена:
Обратная замена:
Уравнение удобно решить на числовой окружности (рис.), т.к. нужно найти кол-во решений. Имеем две серии корней: и
.
Пока мы перемещаемся от левого конца отрезка - точки -п/2 - до правого, т.е. точки 2п (а эта точка совпадает с нулем), мы попадаем в точку -5п/6 единожны, в точку -п/6 - дважды, т.е. корней на отрезке будет 3.
ОТВЕТ: 3.
Приложения:

sofyaglebowa:
Очень прям вот очень большое спасибо♥
Похожие вопросы
Предмет: Русский язык,
автор: yutkina83
Предмет: Русский язык,
автор: ЛизаМарко
Предмет: Другие предметы,
автор: Динулька1
Предмет: История,
автор: yandeks04
Предмет: Математика,
автор: ксюлайв