Предмет: Математика,
автор: Аноним
Исследовать на сходимость ряд!
Приложения:
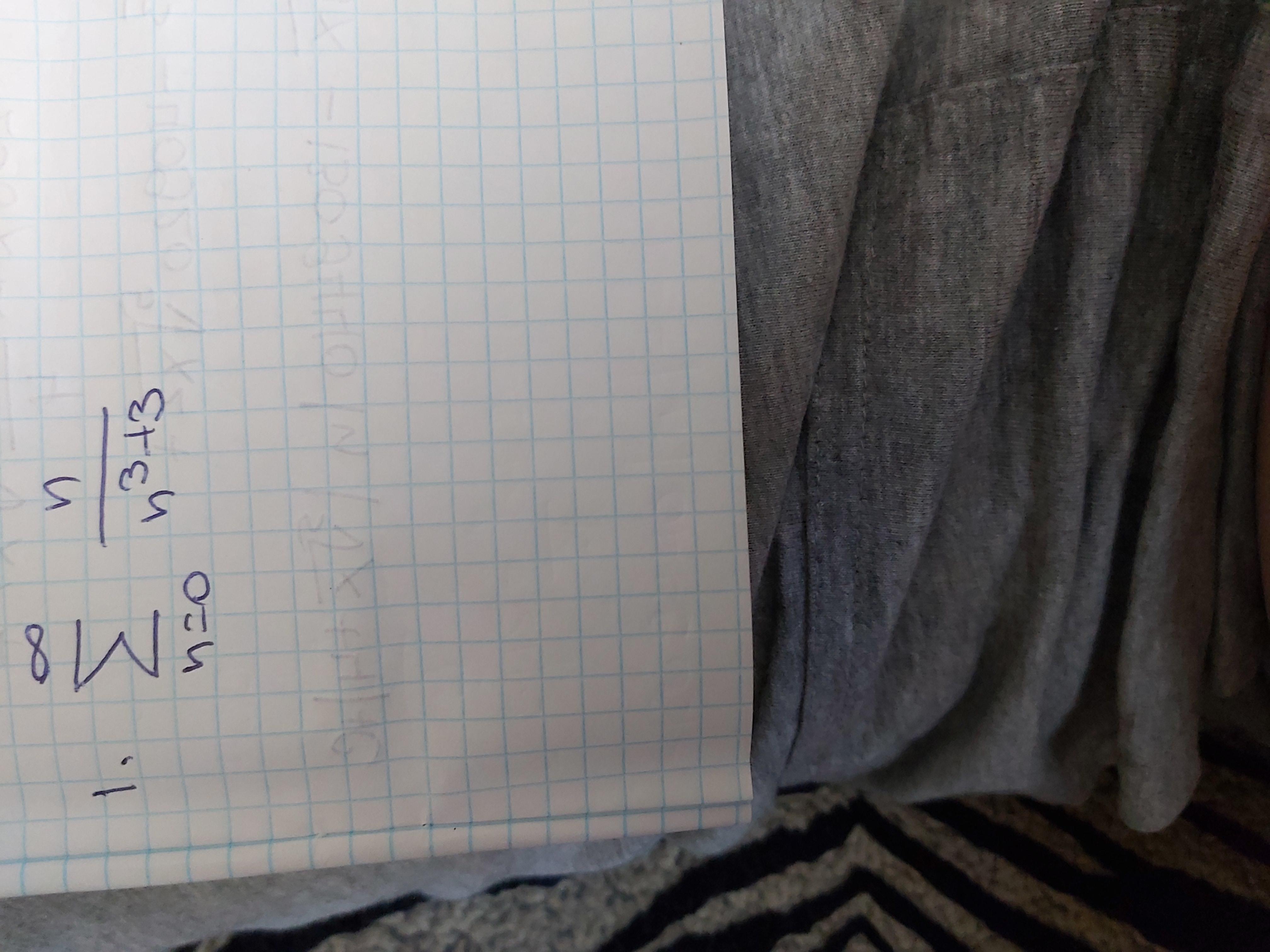
Ответы
Автор ответа:
0
Ответ:
Сходится
Пошаговое объяснение:
Используем признак сравнения (нижний индекс начинается с 1, так как 0 не дает вклада в сумму):
Последний ряд сходится как ряд c показателем степени p>1. Так как исходный ряд ограничен сверху значением суммы этого ряда, то исходный ряд сходится по признаку сравнения.
Похожие вопросы
Предмет: Українська мова,
автор: zzgzgzyulia
Предмет: Қазақ тiлi,
автор: ladysidenko
Предмет: Русский язык,
автор: Lera042002
Предмет: Математика,
автор: 14112009